Vins作为经典的VIO系统,这里记录它的原理和实践。
理论
VINS Fusion简介
VINS Fusion在VINS Mono的基础上,添加了GPS等可以获取全局观测信息的传感器,使得VINS可以利用全局信息消除累计误差,进而减小闭环依赖。此外,全局信息可以使分多次运行的VINS Mono统一到一个坐标系,从而方便协同建图和定位。
Fusion的思路
局部传感器(如相机,IMU,激光雷达等)被广泛应用于建图和定位算法。尽管这些传感器能够在没有GPS信息的区域,实现良好的局部定位和局部建图效果,但是这些传感器只能提供局部观测,限制了其应用场景:
- 第一个问题是局部观测数据缺乏全局约束,当我们每次在不同的位置运行算法时,都会得到不同坐标系下的定位和建图结果,因而难以将这些测量结果结合起来,形成全局效果。
- 第二个问题是基于局部观测的估计算法必然存在累计漂移,尽管回环检测可以一定程度上消除漂移,但是对于数据量较大的大范围场景,算法依然难以处理。 相比于局部传感器,全局传感器(如GPS,气压计和磁力计等)可以提供全局观测。这些传感器使用全局统一坐标系,并且输出的观测数据的方差不随时间累计而增加。但这些传感器也存在一些问题,导致无法直接用于精确定位和建图。以GPS为例,GPS数据通常不平滑,存在噪声,且输出速率低。
因此,一个简单而直观的想法是将局部传感器和全局传感器结合起来,以达到局部精确全局零漂的效果。这也就是VINS Fusion这篇论文的核心内容。
VINS Fusion的算法架构如图所示:
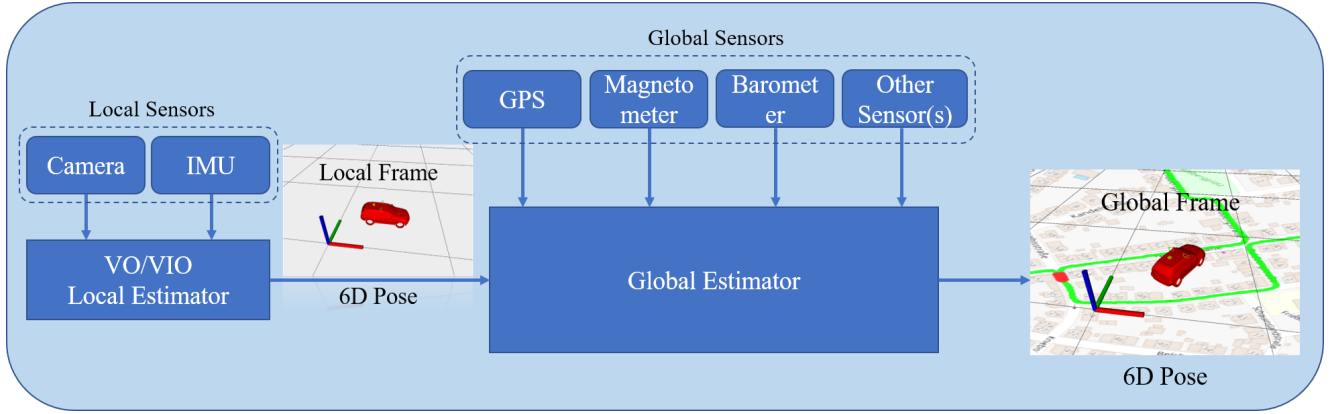
下图以因子图的方式表示观测和状态之间的约束:
其中圆形为状态量(如位姿,速度,偏置等),黄色正方形为局部观测的约束,即来自VO/VIO的相对位姿变换;而其他颜色的正方形为全局观测的约束,比如紫色正方形为来自GPS的约束。
局部约束(残差)的构建参考vins mono论文,计算的是相邻两帧之间的位姿残差。这里只讨论GPS带来的全局约束。首先当然是将GPS坐标,也就是经纬度转换为大地坐标系。习惯上选择右手坐标系,x,y,z轴正方向分别是北东地或东北天方向。接下来就可以计算得到全局约束的残差:
其中 $z$ 为GPS测量值,$X$为状态预测,$h$方程为观测方程。$X$可以通过上一时刻状态以及当前时刻与上一时刻的位姿变换计算出来。具体到本文的方法,就是利用VIO得到当前时刻和上一时刻的相对位姿$dX$,加到上一时刻的位姿上$X(i-1)$,得到当前时刻的位姿$X_i$。需要注意的是,这里的$X$以第一帧为原点。通过观测方程$h$,将当前状态的坐标转换到GPS坐标系下。这样就构建了一个全局约束。
之后的优化就交给BA优化器进行迭代优化,vins fusion沿用了ceres作为优化器。
Fusion实现
GPS和VIO数据输入
需要明确的一点是,VIO的输出是相对于第一帧的累计位姿变换,也就是以第一帧为原点。VINS Fusion接收vio输出的局部位姿变换(相对于第一帧),以及gps输出的经纬度坐标,进行融合。接受数据输入的接口在global_fusion/src/globaOptNode.cpp文件中,接口定义的关键代码如下:
void GPS_callback(const sensor_msgs::NavSatFixConstPtr &GPS_msg)
{
gpsQueue.push(GPS_msg); // 每次接收到的gps消息添加到gpsQueue队列中
}
void vio_callback(const nav_msgs::Odometry::ConstPtr &pose_msg)
{
double t = pose_msg->header.stamp.toSec();
last_vio_t = t;
Eigen::Vector3d vio_t; // 平移矩阵,转换的代码省略
Eigen::Quaterniond vio_q; // 旋转四元数,转换的代码省略
globalEstimator.inputOdom(t, vio_t, vio_q); // 将时间,平移,四元数作为预测添加进globalEstimator
m_buf.lock();
while(!gpsQueue.empty())
{
sensor_msgs::NavSatFixConstPtr GPS_msg = gpsQueue.front();
double gps_t = GPS_msg->header.stamp.toSec();
// 找到和vio里程计数据相差在10ms以内的gps数据,作为匹配数据
if(gps_t >= t - 0.01 && gps_t <= t + 0.01)
{
double latitude = GPS_msg->latitude;
double longitude = GPS_msg->longitude;
double altitude = GPS_msg->altitude;
double pos_accuracy = GPS_msg->position_covariance[0];
globalEstimator.inputGPS(t, latitude, longitude, altitude, pos_accuracy); // 关键,将gps数据作为观测输入到globalEstimator中
gpsQueue.pop(); // 满足条件的gps信息弹出
break;
}
else if(gps_t < t - 0.01)
gpsQueue.pop(); // 将过时的gps信息弹出
else if(gps_t > t + 0.01)
break; // 说明gps信息是后来的,就不要改动gps队列了,退出
}
m_buf.unlock();
// ...其余省略
}
GPS和VIO融合
VINS Fusion融合GPS和VIO数据的代码在global_fusion/src/globalOpt.cpp文件中,下面进行详细介绍。
a. 接收GPS数据,接收VIO数据并转到GPS坐标系
// 接收上面输入的vio数据
void GlobalOptimization::inputOdom(double t, Eigen::Vector3d OdomP, Eigen::Quaterniond OdomQ){
vector<double> localPose{OdomP.x(), OdomP.y(), OdomP.z(),
OdomQ.w(), OdomQ.x(), OdomQ.y(), OdomQ.z()};
localPoseMap[t] = localPose;
// 利用vio的局部坐标进行坐标变换,得到当前帧的全局位姿
Eigen::Quaterniond globalQ;
globalQ = WGPS_T_WVIO.block<3, 3>(0, 0) * OdomQ;
Eigen::Vector3d globalP = WGPS_T_WVIO.block<3, 3>(0, 0) * OdomP + WGPS_T_WVIO.block<3, 1>(0, 3);
vector<double> globalPose{globalP.x(), globalP.y(), globalP.z(),
globalQ.w(), globalQ.x(), globalQ.y(), globalQ.z()};
globalPoseMap[t] = globalPose;
}
// 接收上面输入的gps数据
void GlobalOptimization::inputGPS(double t, double latitude, double longitude, double altitude, double posAccuracy)
{
double xyz[3];
GPS2XYZ(latitude, longitude, altitude, xyz); // 将GPS的经纬度转到地面笛卡尔坐标系
vector<double> tmp{xyz[0], xyz[1], xyz[2], posAccuracy};
GPSPositionMap[t] = tmp;
newGPS = true;
}
上面出现了VIO数据的局部坐标转到GPS坐标的计算过程,其公式如下:
这个公式中的GPS2VIO出现在后面的优化过程中,计算方法为:
b. 融合优化
这里是融合的关键代码,可以看出其流程如下:
- 构建t_array和q_array,用来存入平移和旋转变量,方便输入优化方程,以及在优化后取出。
- 利用RelativeRTError::Create()构建VIO两帧之间的约束,输入优化方程
- 利用TError::Create()构建GPS构成的全局约束,输入优化方程
- 取出优化后的数据
void GlobalOptimization::optimize()
{
while(true)
{
if(newGPS)
{
newGPS = false;
// ceres定义部分略去
// add param
mPoseMap.lock();
int length = localPoseMap.size();
// ********************************************************
// *** 1. 构建t_array, q_array用来存优化变量,等优化后取出 ***
// ********************************************************
double t_array[length][3];
double q_array[length][4];
map<double, vector<double>>::iterator iter;
iter = globalPoseMap.begin();
for (int i = 0; i < length; i++, iter++)
{
// 取出数据部分省略
// 添加了parameterblock
problem.AddParameterBlock(q_array[i], 4, local_parameterization);
problem.AddParameterBlock(t_array[i], 3);
}
map<double, vector<double>>::iterator iterVIO, iterVIONext, iterGPS;
int i = 0;
for (iterVIO = localPoseMap.begin(); iterVIO != localPoseMap.end(); iterVIO++, i++)
{
// ********************************************************
// ********************* 2. VIO约束 *******************
// ********************************************************
iterVIONext = iterVIO;
iterVIONext++;
if(iterVIONext != localPoseMap.end())
{
Eigen::Matrix4d wTi = Eigen::Matrix4d::Identity(); // 第i帧的变换矩阵
Eigen::Matrix4d wTj = Eigen::Matrix4d::Identity(); // 第j帧的变换矩阵
// 取出数据部分省略
Eigen::Matrix4d iTj = wTi.inverse() * wTj; // 第j帧到第i帧的变换矩阵
Eigen::Quaterniond iQj; // 第j帧到第i帧的旋转
iQj = iTj.block<3, 3>(0, 0);
Eigen::Vector3d iPj = iTj.block<3, 1>(0, 3); // 第j帧到第i帧的平移
ceres::CostFunction* vio_function = RelativeRTError::Create(iPj.x(), iPj.y(), iPj.z(),
iQj.w(), iQj.x(), iQj.y(), iQj.z(),
0.1, 0.01);
problem.AddResidualBlock(vio_function, NULL, q_array[i], t_array[i], q_array[i+1], t_array[i+1]);
}
// ********************************************************
// ********************* 3. GPS约束 *******************
// ********************************************************
double t = iterVIO->first;
iterGPS = GPSPositionMap.find(t);
if (iterGPS != GPSPositionMap.end())
{
ceres::CostFunction* gps_function = TError::Create(iterGPS->second[0], iterGPS->second[1],
iterGPS->second[2], iterGPS->second[3]);
problem.AddResidualBlock(gps_function, loss_function, t_array[i]);
}
}
ceres::Solve(options, &problem, &summary);
// ********************************************************
// ******************* 4. 取出优化结果 *****************
// ********************************************************
iter = globalPoseMap.begin();
for (int i = 0; i < length; i++, iter++)
{
// 取出优化结果
vector<double> globalPose{t_array[i][0], t_array[i][1], t_array[i][2],
q_array[i][0], q_array[i][1], q_array[i][2], q_array[i][3]};
iter->second = globalPose;
if(i == length - 1)
{
Eigen::Matrix4d WVIO_T_body = Eigen::Matrix4d::Identity();
Eigen::Matrix4d WGPS_T_body = Eigen::Matrix4d::Identity();
// 剩余的存入部分省略,得到WGPS_T_WVIO
WGPS_T_WVIO = WGPS_T_body * WVIO_T_body.inverse();
}
}
updateGlobalPath();
mPoseMap.unlock();
}
std::chrono::milliseconds dura(2000);
std::this_thread::sleep_for(dura);
}
return;
}
上述代码中出现了一个关键的部分,即WGPS_T_WVIO的计算。从之前的代码中知道,这个4*4矩阵是用来做VIO到GPS坐标系的变换的。按道理讲,这个矩阵应当是不需要反复计算的,毕竟第一帧和GPS的坐标变换是确定的。但是运行结果来看,这个矩阵的值是在变化的,而且有时变化比较大。这里不太懂,知乎刘知(https://zhuanlan.zhihu.com/p/75492883)说是为了避免VIO漂移过大。
GSP和VIO融合总结
使用场景
根据上文中分析的优化策略,global fusion的应用场景应该是GPS频率较低,VIO频率较高的系统。fusion 默认发布频率位10hz,而现在的GPS可以达到20hz,如果在这种系统上使用,你可能还需要修改下VIO或者GPS频率。另外,使用的GPS是常见的误差较大的GPS,并不是RTK-GPS。
GPS与VIO时间不同步
上文提到了,在多传感器融合系统中,传感器往往需要做时钟同步,那么global Fusion需要么?GPS分为为很多种,我们常见的GPS模块精度较低,十几米甚至几十米的误差,这种情况下,同不同步没那么重要了,因为GPS方差太大。另外一种比较常见的是RTK-GPS ,在无遮挡的情况下,室外精度可以达到 2cm之内,输出频率可以达到20hz,这种情况下,不同步时间戳会对系统产生影响,如果VIO要和RTK做松耦合,这点还需要注意。
参考文献
[1] https://blog.csdn.net/u011178262/article/details/88769414
[2] https://zhehangt.github.io/2018/04/24/SLAM/VINS/VINSVIO/
[3] https://www.codetd.com/article/4903500
[4] 沈老师PPT:https://slides.games-cn.org/pdf/GAMES201840%E6%B2%88%E5%8A%AD%E5%8A%BC.pdf
//estimate 代码及推导
[5] https://zhuanlan.zhihu.com/p/61733458
[6] https://cggos.github.io/slam/vinsmono_note_cg.html
[7] https://www.zybuluo.com/Xiaobuyi/note/866099
欧拉积分、中点积分与龙格-库塔积分:
[8] http://liuxiao.org/2018/05/%E6%AC%A7%E6%8B%89%E7%A7%AF%E5%88%86%E3%80%81%E4%B8%AD%E7%82%B9%E7%A7%AF%E5%88%86%E4%B8%8E%E9%BE%99%E6%A0%BC%EF%BC%8D%E5%BA%93%E5%A1%94%E7%A7%AF%E5%88%86/
[9] https://scm_mos.gitlab.io/2019/04/23/VINS-FUSION/
[10] https://zhi-ang.github.io/categories/SLAM/
[11] GPS/VIO https://zhi-ang.github.io/2019/09/11/vins_fusion/
[12] 带有代码流程图:https://www.guyuehome.com/blog/column/id/6 \ https://blog.csdn.net/qq_42700518/category_9544233.html
[13] 简洁的介绍:https://www.sohu.com/a/284064259_715754
[14] https://blog.csdn.net/qq_41839222/article/details/86633487 vins_fusion论文解读
[15] 各个线程的解读:https://blog.csdn.net/moyu123456789/category_8945611.html
[16] https://blog.csdn.net/qq_41839222/article/details/85793998 VINS-Mono论文学习与代码解读——目录与参考
[17] DOC 文档 https://www.researchgate.net/profile/Hongchen-Gao/publication/351245926_Formula_Derivation_and_Code_Analysis_of_VINS-Mono/links/61324f272b40ec7d8be36bee/Formula-Derivation-and-Code-Analysis-of-VINS-Mono.pdf?origin=publication_detail