LeetCode刷题栈使用总结学习笔记。
栈基础知识
栈:先进后出
-
栈只能从表的一端存取数据,另一端封闭。
-
栈的具体实现:
(1)顺序栈:采用数组实现
(2)链栈:采用链式存储结构实现,链表实现
- 顺序栈及基本操作
顺序表模拟栈存储结构常用的实现思路:在顺序表中设定一个实时指向栈顶元素的变量(一般命名为 top),top 初始值为 $-1$,表示栈中没有存储任何数据元素,即栈是”空栈”,一旦有数据元素进栈,则 top 就做 $+1$ 操作,反之,如果数据元素出栈,top 就做 $-1$ 操作。
(1)顺序栈元素进栈,从栈顶进入,实现代码如下:
在想象一个栈的工作方式时,可以想象一下餐厅流水线开始时的一堆盘子。当餐厅的工作人员补充餐盘时,他或她放入的第一个盘子将是最后一个被取走的。
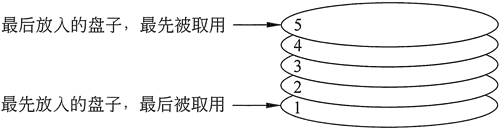
图1
如果某个算法需要**首先处理序列中最后保存的元素**,那么栈对于这种算法而言是非常有用的数据结构。
例如,计算机系统在执行程序时就会使用栈。当某个函数被调用时,计算机系统会将程序的返回地址、函数的参数以及函数的局部变量保存在栈中。当函数返回时,这些局部变量、参数和返回的地址等都将被从栈上删除。
## 栈操作
栈有两个主要操作:入栈(push,也被称为压栈)和出栈(pop,也被称为弹栈)。
入栈操作会导致一个值被存储,或者被压入栈。例如,假设有一个空的整数栈,最多可以保存 3 个值。有了这个栈,则可以执行以下入栈操作:
push(5);
push(10);
push(15);
图 2 显示了在执行这些入栈操作之后的栈状态。

图2
出栈操作将从栈中检索(继而删除)一个值。假设要在如图 2 所示的栈上执行 3 个连续的出栈操作,结果将如图 3 所示。

图3
```c++
/*
栈
*/
#define MaxSize 10 // 栈中元素的最大个数
#include
#include
#include
using namespace std;
typedef int ElemType;
struct SqStack {
ElemType data[MaxSize]; // 静态数组存放栈顶元素
int top; // 栈顶指针
};
// 初始化栈
void InitStack(SqStack &S) { S.top = -1; }
// 判断栈空
bool StackEmpty(SqStack S) {
if (S.top == -1) {
return true;
} else {
return false;
}
}
// 入栈
bool Push(SqStack &S, ElemType x) {
if (S.top == MaxSize - 1) {
return false;
} else {
S.top++;
S.data[S.top] = x; // S.top指向栈顶
return true;
}
}
// 出栈
bool Pop(SqStack &S, ElemType &x) {
if (S.top == -1) { // 栈空
return false;
} else {
x = S.data[S.top--]; // 先赋值再--
return true;
}
}
// 读取栈顶元素
bool GetTop(SqStack S, ElemType &x) {
if (S.top == -1) {
return false;
} else {
x = S.data[S.top];
return true;
}
}
bool DestroyStack(SqStack &S) { S.top = -1; }
int main() {
SqStack S;
InitStack(S); // 初始化
cout << "栈是否为空:" << StackEmpty(S) << endl; // 判空
for (int i = 0; i < 5; i++) {
Push(S, i);
}
ElemType top, pop;
GetTop(S, top);
cout << "栈顶元素:" << top << endl;
Pop(S, pop);
cout << "出栈元素:" << pop << endl;
GetTop(S, top);
cout << "新栈顶元素:" << top << endl;
DestroyStack(S); // 销毁栈
cout << "栈是否为空:" << StackEmpty(S) << endl; // 判空
}
```
## 栈的应用之括号匹配
除了逆序输出问题之外,括号匹配问题也是栈的一个典型应用,即检查表达式中的括号是否完全匹配,例如对于表达式a / ( (b + c) *d 和a / ( (b + c) *d ),前者的括号不匹配而后者的括号匹配。
> 在某个字符串(长度不超过100)中有左括号、右括号和大小写字母:规定(与常见的算数式子一样)任何一个左括号都从内到外与它右边且距离最近的右括号匹配。写一个程序,找到无法匹配的左括号和右括号,输出原来的字符串,并在下一行标出不能匹配的括号。不能匹配的左括号用"$“标注,不能匹配的右括号用”?"标注。
### 算法思想
每个右括号必定要与之前未被匹配的离它最近的一个进行匹配。因此,可以从左至右的顺序遍历整个字符串:
- 遍历过程中如果遇到左括号,就将其放入栈中以待后续右括号的匹配;
- 遇到右括号,若此时栈非空,则栈顶左括号必定和当前右括号匹配;相反,若此时栈为空,则表示当前右括号不存在与之匹配的左括号,右括号匹配失败。
- 当字符串全部遍历完后,若栈非空,表明栈中的左括号不存在与之匹配的右括号,左括号匹配失败。
```c++
#include<bits/stdc++.h>
using namespace std;
stack brackets;
int main(){
string str;
while(cin>>str){
string answer(str.size(),' '); //设为 输入长度个 空格
for(int i=0; i<str.size(); i++){
if(str[i] == '(' ){
brackets.push(i); //压入左括号下标
}else if(str[i] == ')' ){ //如果是右括号
if(!brackets.empty()){
brackets.pop(); //栈不空则弹出,即有左括号匹配
}else{
answer[i] = '?'; //右括号不匹配
}
}
}
while(!brackets.empty()){
answer[brackets.top()] = '$'; //左括号不匹配
brackets.pop();
}
cout<<str<<endl;
cout<<answer<<endl;
}
return 0;
}
```
## 栈的应用之中缀表达式转化为后缀表达式
### 中缀表达式基本概念
中缀表达式:操作符以中缀形式处于操作数的中间,例:$1 + 2$。
后缀表达式:将运算符写在操作数之后,例:$12+$。
一个表达式E的后缀形式可以如下定义:
- 如果$E$是一个变量或常量,则$E$的后缀式是$E$本身。
- 如果$E$是$E_1 op E_2$形式的表达式,这里$op$是任何二元操作符,则E的后缀式为$E_1’$ $E_2’$ $op$,这里$E_1’$和$E_2’$分别为$E_1$和$E_2$的后缀式。
- 如果$E$是$(E_1)$形式的表达式,则$E_1$的后缀式就是$E$的后缀式。
那么为什么要将中缀表达式变为后缀表达式呢?
与后缀表达式相比,中缀表达式不容易被计算机解析,后缀表达式更易于计算机计算。
将一个中缀表达式转换为后缀表达式的一般算法:
中缀转后缀转换过程需要用到栈,具体过程如下:
从左到右扫描字符串
1)如果遇到操作数,我们就直接将其输出 。
2)如果遇到操作符,当栈为空直接进栈,不为空,判断栈顶元素操作符优先级是否比当前操作符小,小的话直接把当前操作符进栈,不小的话栈顶元素出栈输出,直到栈顶元素操作符优先级比当前操作符小
3)遇到左括号时我们也将其放入栈中。
4)如果遇到一个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为止。注意,左括号也要弹出
### 实例及详细过程
```c++
#include "iostream"
#include "queue"
#include "map"
#include "stack"
#include "cstring"
using namespace std;
/**
* 中缀表达式转后缀表达式
* @return
*/
int main(){
char bds[1000];
map<char,int> yxj;
queue q;
stack s;
yxj['*'] = 2;
yxj['/'] = 2;
yxj['+'] = 1;
yxj['-'] = 1;
cin>>bds;
int len = strlen(bds);
for (int i = 0; i <len ; ++i) {
if(bds[i]>='0'&&bds[i]<='9'){//操作数直接进队列中
q.push(bds[i]);
}else if(bds[i] == '(' || s.size() == 0){//左括号直接入栈
s.push(bds[i]);
}else if(bds[i] == ')') {//右括号需要处理到上一个(位置
while(s.top()!='('){
q.push(s.top());s.pop();
}
s.pop();//弹出左括号
}else{//操作符
while(s.size() && yxj[s.top()]>=yxj[bds[i]]){
q.push(s.top());s.pop();
}
s.push(bds[i]);
}
}
while (s.size()){//栈中可能还有操作符,需要输出
q.push(s.top());s.pop();
}
while(q.size()){
cout<<q.front();q.pop();
}
return 0;
}
```
## 栈的应用之表达式求值(不带括号和带括号的表达式求值)
中缀表达式转换为后缀表达式的手工做法为:
- 按照运算符的优先级对所有的运算单位加括号。 例二: ((a/b) + (((c*d) - (e*f))/g))
- 把运算符号移动到对应括号的后面,然后去掉括号。例二: ((ab)/ (((cd)*(ef)*)-g)/+,去掉括号ab/cd*ef*-g/+
> 以(a+b)*c-d为例:
> 第一步先对运算符两边加括号:
> (((a+b)*c)-d)
> 第二步针对每个括号,我们将运算符移动到括号后面:
> (((ab+)c*)d)-
> 第三部去掉括号
> ab+c*d-
设置一个栈,开始时,栈为空,然后从左到右扫描后缀表达式,若遇操作数,则进栈;
若遇运算符,则从栈中退出两个元素,先退出的放到运算符的右边,后退出的 放到运算符左边,运算后的结果再进栈,直到后缀表达式扫描完毕。
此时,栈中仅有一个元素,即为运算的结果。
### 实现
例如:
我们求3.5.2.-*7.+@的值
约定’@’为表达式的结束符号 ‘.’为操作数的结束符号。
核心代码如下:
```c++
stack s;
char c;
int sum = 0;
while(cin>>c && c!='@') {//扫描表达式字符串
if (c >= '0' && c <= '9') {//数字
sum = sum * 10 + c - '0';
} else if (c == '.') {//操作数结束,入栈
s.push(sum);
sum = 0;
} else {//操作符
int y = s.top();
s.pop();
int x = s.top();
s.pop();
s.push(cult(x, y, c));
}
}
cout<<s.top();
```
