LeetCode刷题排序使用总结学习笔记。
一、快速排序算法
快速排序基本思想
快速排序是基于分治的思想实现的。一个有序的序列总可以分为两部分:找一个基准值把序列一分为二,左边的区间中原始值总是小于等于基准值,右边区间中元素值总数大于等于基准值。对左右两个区间采用相同的方法直到子区间的元素个数为1,则每个基准值的位置都已正确归位置。
基本实现思路: ①.选取一个基准值,一般选择起始位置的值。 ②.左右两端开始遍历,右侧区间中找一个小于基准值的位置停下,左侧区间中找一个大于基准值的位置停下,然后交互两个位置的值。 ③.重复②③直到左右指针相遇。 ④.交换基准位置和相遇点的值,使基准值归位。 ⑤.同样方法递归相遇位置的左右两个子区间,直到没个点都归位。 要让右侧指针先走,以使左右指针相遇在小于基准值的点上,然后可以交换到正确的位置。
快速排序代码实现
void qickSort(int left, int right, vector<int>& nums)
{
int i = left;//左指针初始位置
int j = right;//右指针初始位置
if (left > right) return;
int temp = nums[left];//基准数
while (i != j)
{
//右边找一个小于基准数的位置
while (nums[j] >= temp && i < j)
{
j--;
}
//左边找一个大于基准数的位置
while (nums[i] <= temp && i < j)
{
i++;
}
if (i < j)
swap(nums[i],nums[j]);
}
//基准数归位
swap(nums[left],nums[j]);
//递归左右两个子区间
qickSort(left, i - 1, nums);
qickSort(i + 1, right, nums);
}
应用实例
有一个整数数组,请你根据快速排序的思路,找出数组中第 $k$ 大的数。
给定一个整数数组$a$ ,同时给定它的大小$n$和要找的 $k$ ,请返回第 $k$ 大的数(包括重复的元素,不用去重),保证答案存在。
要求:时间复杂度 $O(n\log n)$,空间复杂度 $O(1)$。
示例1
输入:[1,3,5,2,2],5,3
输出:2
解题思路
- 利用快排的思想寻找数组中的第$k$大元素;
- 有重复数字,不用去重,也不用管稳定性与否;
快速排序:每次移动,可以找到一个标杆元素,然后将大于它的移到左边,小于它的移到右边。然后分别对左边和右边进行排序,不断划分左右子段,直到整个数组有序。放到这道题中,如果标杆元素左边刚好有$K -1$个比它大的,那么该元素就是第$K$大,如果它左边 的元素比$K - 1%$多,说明第$K$大在其左边,直接二分,不用管标杆元素右边,同理如果它左边的元素比$K -1$少,那第$K$大在其右边,左边不用管。
-
step 1 :进行一次快排,大元素在左,小元素在右,得到的中轴$p$点。
-
step 2:如果 $p - low + 1 = k$ ,那么$p$点就是第$K$大。
-
step 3:如果 $p - low + 1 > k$,则第$k$大的元素在左半段,更新$high = p - 1$ ,执行 step 1。
-
step 4:如果 $p - low + 1 < k$,则第$k$大的元素在右半段,更新$low = p + 1$, 且 $k = k - (p - low + 1)$,排除掉前面部分更大的元素,再执行step 1。
class Solution {
public:
// 常规的快排划分,但这次是大数在左
int partion(vector<int>& a, int low, int high) {
int temp = a[low];
while (low != high)
{
while (low < high && a[high] <= temp)
high--;
while (low < high && a[low] >= temp)
{
low++;
}
if(low < high)
swap(a[high], a[low]);
}
return low;
}
int quicksort(vector<int>& a, int low, int high, int K) {
int p = partion(a, low, high); // 先进行一轮划分,p下标左边的都比它大,下标右边都比它小
if ( K == p - low + 1) // p刚好是第K个点,则找到
return a[p];
else if (p- low + 1 > K) { // 从头到p超过K个数组,则目标在左边
return quicksort(a, low, p - 1, K); // 递归左边
}
else {
return quicksort(a, p + 1, high, K - (p - low + 1));
}
}
int findKth(vector<int>a, int n, int K) {
return quicksort(a, 0, n - 1, K);
}
};
二、归并排序算法
分治思想
分治就是分而之,面对一个规模复杂的问题,把它分解成一系列的简单子问题,对子问题求解的结果进行合并从而实现对整个问题的求解。 通过不断的递归,每次尽可能的缩小问题的规模,直至满足基线条件;基线条件必须尽可能的简单,最好能直接得到需要结果。比如对一个数组排序,基线条件就是当数组只有一个元素的时候,就认为是有序的,直接返回结果。 快速排序、归并排序都是采用的分治以及递归的思想。
归并排序
将两个有序的数组合并成一个有序数组称为归并。归并排序包含了两个过程: ①:从上往下的分解:把当前区间一分为二,直至分解为若干个长度为1的子数组 ②:从下往上的合并:两个有序的子区域两两向上合并 如下图所示:

归并排序的一般步骤: ①.分解:把当前区间一分为二,分解点即中间点mid = (left+right)/2 ②.求解:分别递归左右两个子区间[left…mid] 和 [mid+1…right]进行归并排序。递归的终结条件是子区间长度为1。 ③.合并:把两个有序子数组合并需要占用一个临时空间,依次挪动两个子区间的指针,比较元素值大小,将较小的值存入临时空间的开头。将两个有序区间归并成一个临时有序区间[left…right],并将结果拷贝到原数组的区间[left…right],使原始数组[left…right]变为有序。
过程分析
当合并左右两个有序区间时,分为以下几种情况: ①.“左区间”、“右区间”都还有元素,当前右区间元素值小时

如上图,右区间中元素 j 小于左区间中元素 i,则元素 j 小于左区间中范围 [i,mid] 中的所有元素。 ②.“左区间”元素用完、“右区间”还剩有元素时

如上图,左区间中元素已经排完,此时右区间中还剩余有元素,此时右区间中元素值全部大于左区间中元素值。 ③.“右区间”元素用完、“左区间”还剩有元素时

如上图,右区间中元素已经排完,此时左区间中还剩余有元素,此时左区间中元素值全部大于右区间中元素值。
void Mergersort(vector<int>& a, int left, int right) {
if (left == right) {
return;
}
int mid = left + (right - left) / 2;
Mergersort(a, left, mid); // 左侧排序
Mergersort(a, mid + 1, right); // 右侧排序
Merge(a, left, mid, right); // 合并
}
void Merge(vector<int>& a, int left, int mid, int right) {
int nums = right - left + 1;
vector<int> help(nums, 0);
int i = 0;
int p1 = left;
int p2 = mid + 1;
while (p1 <= mid && p2 <= right) {
help[i++] = a[p1] <= a[p2] ? a[p1++] : a[p2++];
}
while (p2 <= right)
{
help[i++] = a[p2++];
}
while (p1 <= mid)
{
help[i++] = a[p1++];
}
for (int i = 0; i < nums; i++) {
a[left++] = help[i];
}
}
应用实例
LeetCode - 归并排序 + 索引数组 - 315. 计算右侧小于当前元素的个数
题目 315. 计算右侧小于当前元素的个数
难度 困难
给定一个整数数组 nums,按要求返回一个新数组 counts。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例:
输入: [5,2,6,1]
输出: [2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1).
2 的右侧仅有 1 个更小的元素 (1).
6 的右侧有 1 个更小的元素 (1).
1 的右侧有 0 个更小的元素.
解题思路
普通遍历算法肯定超时,应该思考如何简化算法。 这里采用 归并排序 + 索引数组的算法
整个的思路是这样子的:在归并排序的过程中,统计每个前有序数组中每个数的逆序数个数。
我们首先要知道什么是归并排序,这个在排序算法中有讲,我就不说了。然后要在归并排序的过程中,统计每个数的逆序数的个数。
那么如何统计逆序数的个数呢?我们在归并的时候,总是将数组分割为两部分,然后将两部分进行排序,分为前有序数组和后有序数组。

求解 “逆序对” 的关键在于:当其中一个数字放进最终归并以后的有序数组中的时候,这个数字与之前看过的数字个数(或者是未看过的数字个数)可以直接统计出来,而不必一个一个数。
而本题目的要求是:让我们求 “在一个数组的某个元素的右边,比自己小的元素的个数”
因此,我们就 应该在 “前有序数组” 的元素出列的时候,数一数 “后有序数组” 已经出列了多少元素,因为这些已经出列的元素都比当前出列的元素要小(或者等于)。下面这幅图可能比较好理解。

但是与此同时,我们也发现一个问题,归并排序后,数组的下标会发生变化,那要怎样去定位原始数组的下标呢?这里采用一个索引数组的办法。索引数组的原理是这样的:

也就是说,我们不管归并之后怎么变化,用一个临时数组来记录原数组的下标。这样在统计每个数的数量时候,就能够精确定位
总结: 1、我们借助计算 “逆序数” 的思路完成本题,关键在于这里我们只能在 “前有序数组” 出列的时候计算逆序数;这点很关键,一定要弄清楚逆序数的求法。 如果题目让我们计算 “$nums[i]$ 左侧小于 $nums[i]$ 的元素的数量” 可以在 “后有序数组” 出列的时候计算逆序数; 2、体会 “索引数组” 这个使用技巧。
索引数组
题目中要求的是对每个位置求右侧小于该位置的数组的元素个数,若直接对原数组按数值进行排序,则排序后各元素的位置发生变动,无法和原数组中位置进行对应。 因此可以用原数组的索引值建立新数组,排序时根据索引值获取对应数值进行比较,可以只让索引参与排序。
class Solution {
public:
vector<int> countSmaller(vector<int>& nums) {
vector<int> res(nums.size(),0);//保存结果
vector<int> indexs(nums.size(),0);//索引数组
for(int i = 0;i < indexs.size();i++)//索引赋值
{
indexs[i] = i;
}
vector<int> tempindexs(indexs.size(),0);//临时数组
mergeSort(nums,indexs,tempindexs,res,0,nums.size()-1);
return res;
}
void mergeSort(vector<int>& nums,vector<int>& indexs,vector<int>& tempindexs,vector<int>& res,int left,int right)
{
if( left >= right ) return;
int mid = left + (right - left) /2 ;
mergeSort(nums,indexs,tempindexs,res,left,mid);//前有序数组
mergeSort(nums,indexs,tempindexs,res,mid+1,right);//后有序数组
//合并
int i = left;
int j = mid+1;
int t = 0;
while( i <= mid && j <= right )
{
if( nums[indexs[i]] > nums[indexs[j]] ) // 则 j 对应的数,小于从 i 开始的所有数据
{
for( int k = i;k <= mid ;k++)
{
res[indexs[k]] ++;
}
tempindexs[t++] = indexs[j++];
}
else
{
tempindexs[t++] = indexs[i++];
}
}
while( i <= mid )
{
tempindexs[t++] = indexs[i++];
}
while( j <= right )
{
tempindexs[t++] = indexs[j++];
}
while( left <= right )
{
indexs[left++] = tempindexs[t++];
}
}
};
三、插入排序算法
插入排序基本思想
每一步将一个待排序的数据插入到前面已经排好序的有序序列中,直到插完所有元素为止。
过程分析
算法实现:直接插入排序是将无序序列中的数据插入到有序的序列中,在遍历无序序列时,首先拿无序序列中的首元素去与有序序列中的每一个元素比较并插入到合适的位置,一直到无序序列中的所有元素插完为止。对于一个无序序列$arr{4,6,8,5,9}$来说,我们首先先确定首元素$4$是有序的,然后在无序序列中向右遍历,$6$大于$4$则它插入到$4$的后面,再继续遍历到$8$,$8$大于$6$则插入到$6$的后面,这样继续直到得到有序序列${4,5,6,8,9}$。
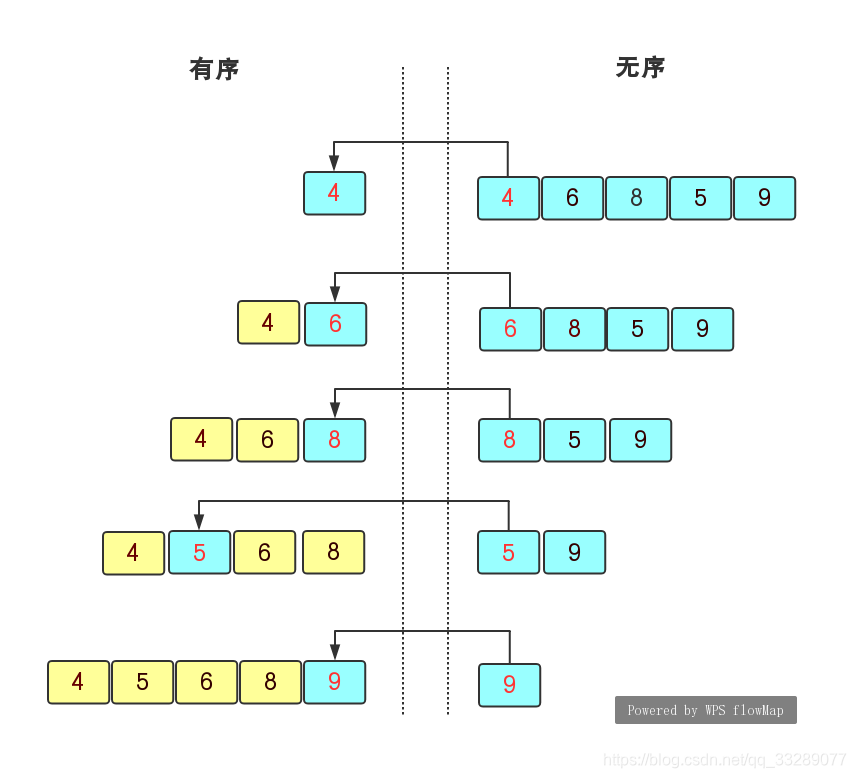
(1)我们用一个变量$tmp$存放关键字,因为我们先确定第一个元素是暂时有序的,所以$tmp$存放无序序列的第二个元素,然后i开始也为第二个元素的下标,j则为$i-1$,因为$j$要用有序的区域元素来与无序的区域元素比较。那么一开始$i=1$,$tmp=6$,$j=0$,因为$6>4$,所以$6$就不用进行插入;然后$i$向右走,$i=2$,$tmp=arr[2]=8$,$j=i-1=1$,$8>6>4$也不用插入。

(2)$i$继续向右走,$i=3$,$tmp=arr[3]=5$,$j=i-1=2$,$5<8$则要将$8$给$5$所在的元素数据,$j$向左走继续遍历有序区域。

(3)当j向右走到$6$时发现$6>tmp=5$,所以将$6$给它右边的第一个值($j+1$的位置),再继续遍历有序区域,$j=0$时发现$4<5$则$j+1$的位置就是$5$该在的位置那么就将$tmp$的值$5$给$j+1$的位置的元素的值。

(4)再继续上面的操作,$i$最后到$9$发现比前面有序区域的元素都大,则不用再插入了,这样就得到了一个有序序列${4,5,6,8,9}$。

代码实现
void Straightsort(vector<int> a) {
int tmp, i, j;
for (int i = 1; i < a.size(); i++) {
tmp = a[i];
for (j = i - 1; j >= 0 && a[j] > tmp; j--) {
a[j + 1] = a[j];
}
a[j + 1] = tmp;
}
}
应用实例
Nowcoder BM48 数据流中的中位数
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流,使用GetMedian()方法获取当前读取数据的中位数。
输入:[5,2,3,4,1,6,7,0,8]
返回值:”5.00 3.50 3.00 3.50 3.00 3.50 4.00 3.50 4.00 “
说明:数据流里面不断吐出的是5,2,3…,则得到的平均数分别为5,(5+2)/2,3…
class Solution {
public:
//记录输入流
vector<int> val;
void Insert(int num) {
if(val.empty())
//val中没有数据,直接加入
val.push_back(num);
//val中有数据,需要插入排序
else{
int i = 0;
//遍历找到插入点
for(; i < val.size(); i++){
if(num <= val[i]){
break;
}
}
val.insert(val.begin() + i, num);
}
}
double GetMedian() {
int n = val.size();
//奇数个数字
if(n % 2 == 1){
//类型转换
return double(val[n / 2]);
}
//偶数个数字
else{
double a = val[n / 2];
double b = val[n / 2 - 1];
return (a + b) / 2;
}
}
};