深入理解STL源码学习笔记

2022-03-11

记录C++ STL源码学习笔记。

STL 简介

0.两个问题

在介绍 STL 之前，先讨论两个问题：为什么要剖析 STL 源代码？如何剖析 STL 源代码？

首先是为什么要剖析 STL 源代码呢？有人会说，会使用 STL 不就行了，为什么一定要知道其内部的机制呢？对于大多数程序猿来说，确实没有必要去阅读或分析 STL 的源代码，但如果要想提升自己的编程修养，要相让自己编码的思想境界提升一个档次，还是很有必要读读 STL 这样的大师制作。阅读和分析之后，你会明白STL是如何分配和管理内存的（特别是对vector、string、deque等动态数据结构），是如何实现各种数据结构（特别是红黑树等比较复杂的数据结构）和相关算法的，又是如何将这些组件融合起来实现高内聚低耦合的。

那么，如何剖析源代码呢？那就是“一层一层一层的剥开”。当然，我这里说的一层一层不是说要一个函数step in 到底，而是说要按层次解读：首先从最外层结构框架着手，从整体上把握；然后从细处着笔，一个组件一个组件的来分析；在分析每个组件时，也是先把握改组件的全貌及其与其他组件的关联关系，然后在深入组件内部，了解其实现。在阅读和分析源码的过程中，首先要理解其功能，然后在看它是如何实现的。切忌纠缠于代码的细节或陷入源码而不能自拔，即坠入“不识庐山真面目，只缘身在此山中”的深渊！

因此，本文的目的在于，站在STL这座大山的山顶，一窥其全貌。随后的文章则深入每个组件，细细观赏每一处的风景。

1.STL 简史

STL 是 Standard Template Library（标准模板库）的缩写。Standard 是指STL是C++标准程序库的一部分，Template是指STL是一套模板，这也是STL最本质的特征。标准模板库使得C++编程语言在有了同Java一样强大的类库的同时，保有了更大的可扩展性。

标准模板库系由 Alexander Stepanov 创造于1979年前后，这也正是 Bjarne Stroustrup 创造C++的年代（非常巧的是，这两为大师都出生于1950年）。

Stepanov早期从事教育工作，在20世纪70年代就开始研究泛型程序设计了。1983年，Stepanov先生转至Polytechnic大学教书，继续研究泛型程序设计，同时写了许多Scheme的程序，应用在graph与network的算法上。1985年又转至GE公司专门教授高级程序设计，并将graph与network的Scheme程序，改用Ada写，用了Ada以后，他发现到一个动态（dynamically）类型的程序（如Scheme）与强制（strongly）类型的程序（如Ada）有多么的不同。在动态类型的程序中，所有类型都可以自由的转换成别的类型，而强制类型的程序却不能。但是，强制类型在出错时较容易发现程序错误。

1988年Stepanov先生转至HP公司运行开发泛型程序库的工作。此时，他已经认识C语言中指针(pointer)的威力，他表示一个程序员只要有些许硬件知识，就很容易接受C语言中指针的观念，同时也了解到C语言的所有数据结构均可以指针间接表示，这点是C与Ada、Scheme的最大不同。Stepanov认为，虽然C++中的继承功能可以表示泛型设计，但终究有个限制。虽然可以在基础类型（superclass）定义算法和接口，但不可能要求所有对象皆是继承这些，而且庞大的继承体系将降低虚拟（virtual）函数的运行效率，这便违反了所谓的“效率”原则。

在C++标准及C++模板概念的标准化过程中，Stepanov参加了许多有关的研讨会，并与C++之父Bjarne讨论模板的设计细节。Stepanov认为C++的函数模板（function template）应该像Ada一样，在声明其函数原型后，应该显式的声明一个函数模板之实例（instance）；Bjarne则不然，他认为可以通过C++的重载（overloading）功能来表达。几经争辩，Stepanov发现Bjarne是对的。

事实上，C++的模板，本身即是一套复杂的宏语言（macro language），宏语言最大的特色为：所有工作在编译时期就已完成。显式的声明函数模板之实例，与直接通过C++的重载功能隐式声明，结果一样，并无很大区别，只是前者加重程序员的负担，使得程序变得累赘。

1992年Meng Lee加入Alex的项目，成为另一位主要贡献者。1992年，HP泛型程序库计划退出，小组解散，只剩下Stepanov先生与Meng Lee小姐（她是东方人，标准模板库的英文名称其实是取STepanov与Lee而来），Lee先前研究的是编译器的制作，对C++的模板很熟，第一版的标准模板库中许多程序都是Lee的杰作。

1993年，Andy Koenig到斯坦福演讲，Stepanov便向他介绍标准模板库，Koenig听后，随即邀请Stepanov参加1993年11月的ANSI/ISO C++标准化会议，并发表演讲。Bell实验室的Andrew Koenig于1993年知道标准模板库研究计划后，邀请Alex于是年11月的ANSI/ISO C++标准委员会会议上展示其观念。并获得与会者热烈的回应。

1994年1月6日，Koenig寄封电子邮件给Stepanov，表示如果Stepanov愿意将标准模板库的说明文件撰写齐全，在1月25日前提出，便可能成为标准C++的一部份。

Alex于是在次年夏天在Waterloo举行的会议前完成其正式的提案，并以百分之八十压倒性多数，一举让这个巨大的计划成为C++ Standard的一部份。

标准模板库于1994年2月年正式成为ANSI/ISO C++的一部份，它的出现，促使C++程序员的思维方式更朝向泛型编程（generic program）发展。

目前，常见的STL实现版本有HP(Hewlett-Packard Company) STL，P.J Plauger版，Rouge Wave版，STLport版，SGI(Silicon Graphics Computer System .Inc) STL版等。

2.STL 六大组件

STL的官方文档将STL划分成了五个主要部分，分别是Containers（容器）、Iterators（迭代器）、Algorithms（算法）、函数对象（Function Objects）、空间分配（Memory Allocation）。而在侯姐的《STL源码剖析》中，还有一个组成部分是Adaptors（适配器）。本文也按照侯捷的规范将STL分为六个部分，而且介绍的顺序也按照他的书中的顺序来介绍。

2.1 Memory Allocation

负责空间配置与管理，本质是实现动态空间配置、空间管理、空间释放的一系列class template。它是容器的底层接口，实际使用STL的用户是看不到Allocation的。

2.2 Iterators

迭代器扮演容器与算法之间的胶合剂，可以形象的理解为“泛型指针”。从实现的角度看，迭代器是一种将operator*、operator->、operator++、operator–等指针相关操作进行重载的class template。所有的STL容器都有自己专属的迭代器——是的，只有容器设计者才知道如何遍历自己的元素，原生指针（Native pointer）也是一迭代器。

2.3 Containers

容器可以理解为各种数据结构，如vector、list、deque、set、map等用来存放特定结构的数据的容器，也是一系列的class template。对于普通用户而言，容器是最熟悉不过了，我们最经常使用的容器主要有 vector, queue, stack, deque, map。相信很多人对 STL 的接触是从使用容器开始的，也有很多人对 STL 印象最深刻的就是容器了。

2.4 Algorithm

主要是各种常用的算法，如sort、search、copy、erase、unique等。从实现的角度看，STL算法是一种function template。其中 sort 相信很多人并不陌生，在很多算法中我们都需要对数据进行排序。

2.5 Function Objects

函数对象的行为类似函数，但可作为算法的某种策略（policy）。从实现的角度看，函数对象是一种重载了operator()（函数调用操作符）的class或class template。

2.6 Adaptors

适配器是一种用来修饰容器或函数对象或迭代器的东西。例如，STL 提供queue和stack，虽然他们看似容器，但其实只能算是一种容器适配器，因为他们的底层实现完全借助于deque，所有的操作都由底层deque提供。改变functor/container/iterator的接口者称为functor/container/iterator adaptor。

3. STL 各组件间的关系

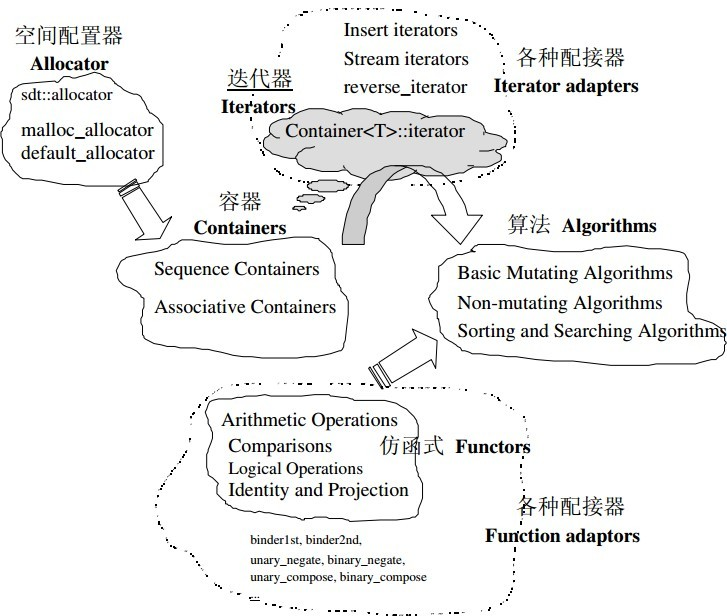
STL 六大组件间的关系如下图：

其中 Container 通过 Allocator 取得数据存储空间，Alogrithm 通过 Iterator 存取 Container 内容，Functor 可以协助 Algorithm 完成不同的策略变化，Adapter 可以修饰或套接 Functor。这里的描述有些抽象，等详细了解了每个组件的功能职责后，就比较好懂了。

4. SGI STL源码结构

最后，这里简单介绍一下SGI STL 源码的结构。我下载的是SGI-STL-v3.3，它是基于1994年HP版STL改造而成的，最新版本v3.3的更新时间是2000年6月8日，共91个文件（SGI-STL官网文档中只列出了90个文件，少列了vector.h这个文件），1.1M大小（其实总代码量并不是很大，非常轻量级 (∧-∧) ，比较适合拿来彻底分析一遍）。

在这91个文件中，有37个以 stl_ 开头的文件，这些都是STL内部实现文件。有23个无扩展名的文件，这些都是STL对外提供的标准接口。有11个与无扩展名文件同名的.h文件，这是对应的old-style形式的头文件（至于为什么不是每个无扩展名（new-style）头文件都有对应的 .h 文件，我也不太清楚）。还有20个文件，主要是为 stl_ 开头的文件提供比较 common 的功能，如 algobase.h、hashtable.h 等，或者是对 stl_ 开头的文件进行一次内部封装，还有其他一些杂项功能等。

5. 参考及推荐

源码阅读与分析工具

能在Linux下用熟练使用vim最好了，实在不行用 Code::Blocks 也挺不错的，可以查找函数原型、定义、调用等。在Windows下用Source Insight最好了，可惜不是免费的，但同样也可以用Code::Blocks 或 Visual C++ Express 等 IDE。原本想用一个UML建模工具来分析一下STL中的类之间的关系的，但是看了看源代码，基本没有太多的继承之类的关系，而且很多UML工具对C++源码自动生成类图的功能支持得并不好，就放弃了。

参考

[1] Wiki: Standard Template Library [2] Wiki: 标准模板库 [3] Standard Template Library Programmer’s Guide [4] 如何看懂源代码–(分析源代码方法)

STL 空间配置器

在STL中，Memory Allocator 处于最底层的位置，为一切的 Container 提供存储服务，是一切其他组件的基石。对于一般使用 STL 的用户而言，Allocator 是不可见的，如果需要对 STL 进行扩展，如编写自定义的容器，就需要调用 Allocator 的内存分配函数进行空间配置。本文涉及到的 SGI STL 源代码文件有 alloc.h, stl_config.h, stl_alloc.h, stl_threads.h 这4个。

在C++中，一个对象的内存配置和释放一般都包含两个步骤，对于内存的配置，首先是调用operator new来配置内存，然后调用对象的类的构造函数进行初始化；而对于内存释放，首先是调用析构函数，然后调用 operator delete进行释放。如以下代码：

class Foo { ... }; 
Foo* pf = new Foo; 
... 
delete pf;

1. Allocator 的标准接口

在 SGI STL 中，Allocator的实现主要在文件alloc.h 和 stl_alloc.h 文件中。根据 STL 规范，Allocator 需提供如下的一些接口（见 stl_alloc.h 文件的第588行开始的class template allocator）：

// 标识数据类型的成员变量，关于中间的6个变量的涵义见后续文章（关于Traits编程技巧）
typedef alloc _Alloc;
typedef size_t     size_type;
typedef ptrdiff_t  difference_type;
typedef _Tp*       pointer;
typedef const _Tp* const_pointer;
typedef _Tp&       reference;
typedef const _Tp& const_reference;
typedef _Tp        value_type;
template <class _Tp1> struct rebind {
  typedef allocator<_Tp1> other;
}; // 一个嵌套的class template，仅包含一个成员变量 other
// 成员函数
allocator() __STL_NOTHROW {}  // 默认构造函数，其中__STL_NOTHROW 在 stl_config.h中定义，要么为空，要么为 throw()
allocator(const allocator&) __STL_NOTHROW {}  // 拷贝构造函数
template <class _Tp1> allocator(const allocator<_Tp1>&) __STL_NOTHROW {} // 泛化的拷贝构造函数
~allocator() __STL_NOTHROW {} // 析构函数
pointer address(reference __x) const { return &__x; } // 返回对象的地址
const_pointer address(const_reference __x) const { return &__x; }  // 返回const对象的地址
_Tp* allocate(size_type __n, const void* = 0) {
  return __n != 0 ? static_cast<_Tp*>(_Alloc::allocate(__n * sizeof(_Tp))) : 0;
  // 配置空间，如果申请的空间块数不为0，那么调用 _Alloc 也即 alloc 的 allocate 函数来分配内存，
} //这里的 alloc 在 SGI STL 中默认使用的是__default_alloc_template<__NODE_ALLOCATOR_THREADS, 0>这个实现（见第402行）
void deallocate(pointer __p, size_type __n) { _Alloc::deallocate(__p, __n * sizeof(_Tp)); } // 释放空间
size_type max_size() const __STL_NOTHROW  // max_size() 函数，返回可成功配置的最大值
    { return size_t(-1) / sizeof(_Tp); }  //这里没看懂，这里的size_t(-1)是什么意思？
void construct(pointer __p, const _Tp& __val) { new(__p) _Tp(__val); } // 调用 new 来给新变量分配空间并赋值
void destroy(pointer __p) { __p->~_Tp(); } // 调用 _Tp 的析构函数来释放空间

在SGI STL中设计了如下几个空间分配的 class template：

template <int __inst> class __malloc_alloc_template // Malloc-based allocator.  Typically slower than default alloc
typedef __malloc_alloc_template<0> malloc_alloc
template<class _Tp, class _Alloc> class simple_alloc
template <class _Alloc> class debug_alloc
template <bool threads, int inst> class __default_alloc_template // Default node allocator.
typedef __default_alloc_template<__NODE_ALLOCATOR_THREADS, 0> alloc
typedef __default_alloc_template<false, 0> single_client_alloc
template <class _Tp>class allocator
template<>class allocator<void>
template <class _Tp, class _Alloc>struct __allocator
template <class _Alloc>class __allocator<void, _Alloc>

其中simple_alloc , debug_alloc , allocator 和 __allocator 的实现都比较简单，都是对其他适配器的一个简单封装（因为实际上还是调用其他配置器的方法，如 _Alloc::allocate ）。而真正内容比较充实的是 __malloc_alloc_template 和 __default_alloc_template 这两个配置器，这两个配置器就是 SGI STL 配置器的精华所在。其中 __malloc_alloc_template 是SGI STL 的第一层配置器，只是对系统的 malloc , realloc 函数的一个简单封装，并考虑到了分配失败后的异常处理。而 __default_alloc_template 是SGI STL 的第二层配置器，在第一层配置器的基础上还考虑了内存碎片的问题，通过内置一个轻量级的内存池。下文将先介绍第一级配置器的异常处理机制，然后介绍第二级配置器的内存池实现，及在多线程环境下内存池互斥访问的机制。

2. SGI STL 内存分配失败的异常处理

内存分配失败一般是由于out-of-memory(oom)，SGI STL 本身并不会去处理oom问题，而只是提供一个 private 的函数指针成员和一个 public 的设置该函数指针的方法，让用户来自定义异常处理逻辑：

private:
#ifndef __STL_STATIC_TEMPLATE_MEMBER_BUG
  static void (* __malloc_alloc_oom_handler)();  // 函数指针
#endif
public:
  static void (* __set_malloc_handler(void (*__f)()))() // 设置函数指针的public方法
  {
    void (* __old)() = __malloc_alloc_oom_handler;
    __malloc_alloc_oom_handler = __f;
    return(__old);
  }

如果用户没有调用该方法来设置异常处理函数，那么就不做任何异常处理，仅仅是想标准错误流输出一句out of memory并退出程序（对于使用new和C++特性的情况而言，则是抛出一个std::bad_alloc()异常），因为该函数指针的缺省值为0，此时对应的异常处理是 __THROW_BAD_ALLOC：

// line 152 ~ 155
#ifndef __STL_STATIC_TEMPLATE_MEMBER_BUG
template <int __inst>
void (* __malloc_alloc_template<__inst>::__malloc_alloc_oom_handler)() = 0;
#endif
// in _S_oom_malloc and _S_oom_realloc
__my_malloc_handler = __malloc_alloc_oom_handler;
if (0 == __my_malloc_handler) { __THROW_BAD_ALLOC; }
// in preprocess, line 41 ~ 50
#ifndef __THROW_BAD_ALLOC
#  if defined(__STL_NO_BAD_ALLOC) || !defined(__STL_USE_EXCEPTIONS)
#    include <stdio.h>
#    include <stdlib.h>
#    define __THROW_BAD_ALLOC fprintf(stderr, "out of memory\n"); exit(1)
#  else /* Standard conforming out-of-memory handling */
#    include <new>
#    define __THROW_BAD_ALLOC throw std::bad_alloc()
#  endif
#endif

SGI STL 内存配置失败的异常处理机制就是这样子了，提供一个默认的处理方法，也留有一个用户自定义处理异常的接口。

3. SGI STL 内置轻量级内存池的实现

第一级配置器 __malloc_alloc_template 仅仅只是对 malloc 的一层封装，没有考虑可能出现的内存碎片化问题。内存碎片化问题在大量申请小块内存是可能非常严重，最终导致碎片化的空闲内存无法充分利用。SGI 于是在第二级配置器 __default_alloc_template 中内置了一个轻量级的内存池。对于小内存块的申请，从内置的内存池中分配。然后维护一些空闲内存块的链表（简记为空闲链表，free list），小块内存使用完后都回收到空闲链表中，这样如果新来一个小内存块申请，如果对应的空闲链表不为空，就可以从空闲链表中分配空间给用户。具体而言SGI默认最大的小块内存大小为128bytes，并设置了128/8=16 个free list，每个list 分别维护大小为 8, 16, 24, …, 128bytes 的空间内存块（均为8的整数倍），如果用户申请的空间大小不足8的倍数，则向上取整。

SGI STL内置内存池的实现请看 __default_alloc_template 中被定义为 private 的这些成员变量和方法（去掉了部分预处理代码和互斥处理的代码）：

private:
#if ! (defined(__SUNPRO_CC) || defined(__GNUC__))
    enum {_ALIGN = 8}; // 对齐大小
    enum {_MAX_BYTES = 128}; // 最大有内置内存池来分配的内存大小
    enum {_NFREELISTS = 16}; // _MAX_BYTES/_ALIGN  // 空闲链表个数
# endif
  static size_t  _S_round_up(size_t __bytes) // 不是8的倍数，向上取整
    { return (((__bytes) + (size_t) _ALIGN-1) & ~((size_t) _ALIGN - 1)); }
__PRIVATE:
  union _Obj { // 空闲链表的每个node的定义
        union _Obj* _M_free_list_link;
        char _M_client_data[1];   };
  static _Obj* __STL_VOLATILE _S_free_list[]; // 空闲链表数组
  static size_t _S_freelist_index(size_t __bytes) { // __bytes 对应的free list的index
        return (((__bytes) + (size_t)_ALIGN-1)/(size_t)_ALIGN - 1);
  }
  static void* _S_refill(size_t __n); // 从内存池中申请空间并构建free list，然后从free list中分配空间给用户
  static char* _S_chunk_alloc(size_t __size, int& __nobjs); // 从内存池中分配空间
  static char* _S_start_free;  // 内存池空闲部分的起始地址
  static char* _S_end_free; // 内存池结束地址
  static size_t _S_heap_size; // 内存池堆大小，主要用于配置内存池的大小

其中 _S_refill 和 _S_chunk_alloc 这两个函数是该内存池机制的核心。 __default_alloc_template 对外提供的 public 的接口有 allocate, deallocate 和 reallocate 这三个，其中涉及内存分配的 allocate 和 reallocate 的逻辑思路是，首先看申请的size（已round up）对应的free list是否为空，如果为空，则调用 _S_refill 来分配，否则直接从对应的free list中分配。而 deallocate 的逻辑是直接将空间插入到相应free list的最前面。

函数 _S_refill 的逻辑是，先调用 _S_chunk_alloc 从内存池中分配20块小内存（而不是用户申请的1块），将这20块中的第一块返回给用户，而将剩下的19块依次链接，构建一个free list。这样下次再申请同样大小的内存就不用再从内存池中取了。有了 _S_refill ，用户申请空间时，就不是直接从内存池中取了，而是从 free list 中取。因此 allocate 和 reallocate 在相应的free list为空时都只需直接调用 _S_refill 就行了。

这里默认是依次申请20块，但如果内存池空间不足以分配20块时，会尽量分配足够多的块，这些处理都在 _S_chunk_alloc 函数中。该函数的处理逻辑如下（源代码这里就不贴了）：

能够分配20块

从内存池分配20块出来，改变 _S_start_free 的值，返回分配出来的内存的起始地址

不足以分配20块，但至少能分配一块

分配经量多的块数，改变 _S_start_free 的值，返回分配出来的内存的起始地址

一块也分配不了

首先计算新内存池大小 size_t __bytes_to_get = 2 * __total_bytes + _S_round_up(_S_heap_size >> 4)，将现在内存池中剩余空间插入到适当的free list中，调用 malloc 来获取一大片空间作为新的内存池：

如果分配成功，则调整 _S_end_free 和 _S_heap_size 的值，并重新调用自身，从新的内存池中给用户分配空间；
否则，分配失败，考虑从比当前申请的空间大的free list中分配空间，如果无法找不到这样的非空free list，则调用第一级配置器的allocate，看oom机制能否解决问题

SGI STL的轻量级内存池的实现就是酱紫了，其实并不复杂。

4. SGI STL 内存池在多线程下的互斥访问

最后，我们来看看SGI STL中如何处理多线程下对内存池互斥访问的（实际上是对相应的free list进行互斥访问，这里访问是只需要对free list进行修改的访问操作）。在SGI的第二级配置器中与内存池互斥访问相关的就是 _Lock 这个类了，它仅仅只包含一个构造函数和一个析构函数，但这两个函数足够了。在构造函数中对内存池加锁，在析构函数中对内存池解锁：

//// in __default_alloc_template
# ifdef __STL_THREADS
    static _STL_mutex_lock _S_node_allocator_lock; // 互斥锁变量
# endif
class _Lock {
    public:
        _Lock() { __NODE_ALLOCATOR_LOCK; }
        ~_Lock() { __NODE_ALLOCATOR_UNLOCK; }
};
//// in preprocess
#ifdef __STL_THREADS
# include <stl_threads.h> // stl 的线程，只是对linux或windows线程的一个封装
# define __NODE_ALLOCATOR_THREADS true
# ifdef __STL_SGI_THREADS
#   define __NODE_ALLOCATOR_LOCK if (threads && __us_rsthread_malloc) \
                { _S_node_allocator_lock._M_acquire_lock(); }  // 获取锁
#   define __NODE_ALLOCATOR_UNLOCK if (threads && __us_rsthread_malloc) \
                { _S_node_allocator_lock._M_release_lock(); }  // 释放锁
# else /* !__STL_SGI_THREADS */
#   define __NODE_ALLOCATOR_LOCK \
        { if (threads) _S_node_allocator_lock._M_acquire_lock(); }
#   define __NODE_ALLOCATOR_UNLOCK \
        { if (threads) _S_node_allocator_lock._M_release_lock(); }
# endif
#else /* !__STL_THREADS */
#   define __NODE_ALLOCATOR_LOCK
#   define __NODE_ALLOCATOR_UNLOCK
#   define __NODE_ALLOCATOR_THREADS false
#endif

由于在 __default_alloc_template 的对外接口中，只有 allocate 和 deallocate 中直接涉及到对free list进行修改的操作，所以在这两个函数中，在对free list进行修改之前，都要实例化一个 _Lock 的对象 __lock_instance ，此时调用构造函数进行加锁，当函数结束时，的对象 __lock_instance 自动析构，释放锁。这样，在多线程下，可以保证free list的一致性。

STL 迭代器

本文涉及到 SGI STL 源码的文件有 iterator.h, stl_iterator_base.h, concept_checks.h, stl_iterator.h, type_traits.h, stl_construct.h, stl_raw_storage_iter.h 等7个文件。

1. 迭代器的设计思维

迭代器（iterators）是一种抽象的设计概念，显示程序中并没有直接对应于这个概念的实体。在 Design Patterns 一书中，对 iterators 模式的定义如下：提供一种方法，使之能够依序遍历某个聚合物（容器）所包含的各个元素，而又无需暴露该聚合物内部的表述方式。

在STL中迭代器扮演着重要的角色。STL的中心思想在于：将数据容器（container）和算法（algorithm）分开，彼此独立设计，最后再通过某种方式将他们衔接在一起。容器和算法的泛型化，从技术的角度来看并不困难，C++ 的 class template 和 function template 可以分别达到目标，难点在于如何设计二者之间的衔接器。

在STL中，起者这种衔接作用的是迭代器，它是一种行为类似指针的对象。指针的各种行为中最常见也最重要的便是内容获取（dereference）和成员访问（member access），因此迭代器最重要的工作就是对 operator* 和 operator-> 进行重载。然而要对这两个操作符进行重载，就需要对容器内部的对象的数据类型和存储结构有所了解，于是在 STL 中迭代器的最终实现都是由容器本身来实现的，每种容器都有自己的迭代器实现，例如我们使用vector容器的迭代器的时候是这样用的 vector<int>::iterator it; 。而本文所讨论的迭代器是不依存于特定容器的迭代器，它在STL中主要有以下两个方面的作用（我自己的理解和总结）：

规定容器中需要实现的迭代器的类型及每种迭代器的标准接口

通过Traits编程技巧实现迭代器相应型别的获取，弥补 C++ 模板参数推导的不足，为配置器提供可以获取容器中对象型别的接口

其中前一个没啥好解释的。关于第二个，后面第3节会详细介绍，那就是Traits编程技巧。

2. STL 迭代器的分类与标准接口

2.1 STL 迭代器的分类

在SGI STL中迭代器按照移动特性与读写方式分为 input_iterator, output_iterator, forward_iterator, bidirectional_iterator, random_access_iterator 这5种，他们的定义都在 stl_iterators_base.h 文件中。这5种迭代器的特性如下：

input_iterator: 这种迭代器所指对象只允许读取，而不允许改变，是只读的（read only）。
output_iterator: 与上面的相反，只能写（write only）。
forward_iterator: 同时允许读和写，适用于 replace() 等算法。
bidirectional_iterator: 可双向移动，即既可以按顺序访问，也可以按逆序访问。
random_access_iterator: 前4种只提供一部分指针运算功能，如前3种只支持 operator++, 而第4种还支持 operator--, 但这种随机访问迭代器还支持 p+n, p-n, p[n], p1-p2, p1+p2 等。

从以上的特性可以看出，input_iterator 和 output_iterator 都是特殊的 forward_iterator, 而 forward_iterator 是特殊的 bidirectional_iterator, bidirectional_iterator 是特殊的 random_access_iterator 。在 stl_iterator_base.h 文件中，他们的定义中我们并不能看到这种特性的表达，而只是规定了这几种迭代器类型及应该包含的成员属性，真正表达这些迭代器不同特性的代码在 stl_iterator.h 文件中。在 stl_iterator_base.h 文件中，除了对这几种迭代器类型进行规定之外，还提供了获取迭代器类型的接口、获取迭代器中的 value_type 类型、获取迭代器中的 distance_type 、获取两个迭代器的距离（distance 函数）、将迭代器向前推进距离 n （advance 函数）等标准接口。

2.2 STL迭代器的标准接口

在 stl_iterator.h 文件中，设计了 back_insert_iterator, front_insert_iterator, insert_iterator, reverse_bidirectional_iterator, reverse_iterator, istream_iterator, ostream_iterator, 等标准的迭代器，其中前3中都使用 output_iterator 的只写特性（只进行插入操作，只是插入的位置不同而已），而第4种使用的是 bidirectional_iterator 的双向访问特性，第5种使用的是 random_access_iterator 的随机访问特性。而最后两种标准迭代器分别是使用 input_iterator 和 output_iterator 特性的迭代器。从这几个标准的迭代器的定义中可以看出，主要是实现了 operator=, operator*, operator->, operator==, operator++, operator--, operator+, operator-, operator+=, operator-= 等指针操作的标准接口。根据定义的操作符的不同，就是不同类型的迭代器了。

例如，下面是 back_insert_iterator 的标准定义：

template <class _Container>
class back_insert_iterator {
protected:
  _Container* container;
public:
  // member variables
  typedef _Container          container_type;
  typedef output_iterator_tag iterator_category;
  typedef void                value_type;
  typedef void                difference_type;
  typedef void                pointer;
  typedef void                reference;
  // member functions, mainly about operator overloading
  explicit back_insert_iterator(_Container& __x) : container(&__x) {}
  back_insert_iterator<_Container>&
  operator=(const typename _Container::value_type& __value) {
    container->push_back(__value);
    return *this;
  }
  back_insert_iterator<_Container>& operator*() { return *this; }
  back_insert_iterator<_Container>& operator++() { return *this; }
  back_insert_iterator<_Container>& operator++(int) { return *this; }
};

3. 迭代器相应型别与Traits编程技巧

3.1 迭代器相应型别

在算法中运用迭代器是，很可能需要获取器相应型别，即迭代器所指对象的类型。此时需要使用到 function template 的参数推导（argument deducation）机制，在传入迭代器模板类型的同时，传入迭代器所指对象的模板类型，例如：

template<class I, class T>
void func_impl(I iter, T t){
    // TODO: Add your code here
}

这里不仅要传入类型 class I, 还要传入类型 class T。然而，迭代器的相应型别并不仅仅只有 “迭代器所指对象的类型” 这一种，例如在STL中就有如下5种：

value_type: 迭代器所指对象的类型。
difference_type: 表示两个迭代器之间的距离，因此也可以用来表示一个容器的最大容量。例如一个提供计数功能的泛型算法 count() ，其返回值的类型就是迭代器的 difference_type .
reference_type: 从迭代器所指内容是否允许修改来看，迭代器分为 constant iterator 和 mutable iterator，如果传回一个可以修改的对象，一般是以 reference 的方式，因此需要传回引用时，使用此类型。
pointer_type: 在需要传回迭代器所指对象的地址时，使用这种类型。
iterator_category: 即前面提到5种的迭代器的类型。

而且实际当中，并不是所有情况都可以通过以上的 template 的参数推导机制来实现（例如算法返回值的类型是迭代器所指对象的类型，template参数推导机制无法推导返回值类型），因此需要更一般化的解决方案，在STL中，这就是Traits编程技巧。

3.2 Traits 编程技巧

在STL的每个标准迭代器中，都定义了5个迭代器相应型别的成员变量，在STL定义了一个统一的接口：

// In file stl_iterator_base.h
template <class _Category, class _Tp, class _Distance = ptrdiff_t,
          class _Pointer = _Tp*, class _Reference = _Tp&>
struct iterator {
  typedef _Category  iterator_category;
  typedef _Tp        value_type;
  typedef _Distance  difference_type;
  typedef _Pointer   pointer;
  typedef _Reference reference;
};

其他的迭代器都可以继承这个标注类，由于后面3个模板参数都有默认值，因此新的迭代器只需提供前两个参数即可（但在SGI STL中并没有使用继承机制）。这样在使用该迭代器的泛型算法中，可以返回这5种类型中的任意一种，而不需要依赖于 template 参数推导的机制。

在SGI STL中，如果启用 __STL_CLASS_PARTIAL_SPECIALIZATION 这个宏定义，还有这样一个标准的 iterator_traits ：

// In file stl_iterator_base.h
template <class _Iterator>
struct iterator_traits {
  typedef typename _Iterator::iterator_category iterator_category;
  typedef typename _Iterator::value_type        value_type;
  typedef typename _Iterator::difference_type   difference_type;
  typedef typename _Iterator::pointer           pointer;
  typedef typename _Iterator::reference         reference;
};

值得一提的是，这些类型不仅可以是泛型算法的返回值类型，还可以是传入参数的类型。例如 iterator_category 可以作为迭代器的接口 advance() 和 distance() 的传入参数之一。不同类型的迭代器实现同一算法的方式可能不同，可以通过这个参数类型来区分不同的重载函数。

4. SGI 中的 __type_traits

traits 编程技巧非常赞，适度弥补了 C++ template 本身的不足。 STL 只对迭代器加以规范，设计了 iterator_traits 这样的东西，SGI进一步将这种技法扩展到了迭代器之外，于是有了所谓的 __type_traits。

在SGI中， __type_traits 可以获取一些类型的特殊属性，如该类型是否具备 trivial default ctor？是否具备 trivial copy ctor？是否具备 trivial assignment operator？是否具备 tivial dtor？是否是 plain old data（POD）？如果答案是肯定的，那么我们对这些类型进行构造、析构、拷贝、赋值等操作时，就可以采用比较有效的方法，如不调用该类型的默认构造、析构函数，而是直接调用 malloc(), free(), memcpy() 等等，这对于大量而频繁的操作容器，效率有显著的提升。

SGI中 __type_traits 的特性的实现都在 type_traits.h 文件中。其中将 bool, char, short, int, long, float, double 等基本的数据类型及其相应的指针类型的这些特性都定义为 __true_type，这以为着，这些对基本类型进行构造、析构、拷贝、赋值等操作时，都是使用系统函数进行的。而除了这些类型之外的其他类型，除非用户指定了它的这些特性为 __true_type，默认都是 __false_type 的，不能直接调用系统函数来进行内存配置或赋值等，而需要调用该类型的构造函数、拷贝构造函数等。

另外，用户在自定义类型时，究竟一个 class 什么时候应该是 __false_type 的呢？一个简单的判断标准是：如果 class 内部有指针成员并需要对其进行动态配置内存是，这个 class 就需要定义为 __false_type的，需要给该类型定义构造函数、拷贝构造函数、析构函数等等。

STL 容器

序列式容器之vector

本文涉及到 SGI STL 源码的文件有vector、stl_vector.h、vector.h 等几个文件。

1. 容器

在数据结构的课程中，我们主要研究数据的特定排列方式，以利于搜索、排序等算法，几乎可以说，任何特定的数据结构都是为了实现某种特定的算法。STL 容器即由一个个特定的数据结构组成，例如向量（vector），链表（list），堆栈（stack），队列（queue），树（tree），哈希表（hash table），集合（set），映射（map）等，根据数据在容器中的排列特性，这些数据接口分为序列式容器（sequence container）和关联式容器（association container）两种，本文主要解读SGI STL中的序列式容器。

所谓序列式容器，其中的元素可序（ordered），但未必有序（sorted）。C++ 本身提供了一个序列式容器——数组（array），STL中还提供了向量（vector），链表（list），堆栈（stack），队列（queue），优先队列（priority queue）等，其中stack和queue只是将deque（双端队列）设限而得到的，技术上可以被归为一种配接器（adaptor）。本系列文章将依次解读SGI STL各容器的关键实现细节。

2. vector 及其数据结构

在STL中，vector的空间在物理上就是连续的，而且是可以动态扩展的，这里的动态扩展，不需要用户去处理溢出的问题，而只需要关心上层逻辑。vector连续物理空间的动态扩展技术是该容器的关键，它主要分为三个步骤：配置新空间，数据移动，释放旧空间。这三个步骤执行的次数以及每次执行时的效率是影响最终 vector 效率的关键因素。为了减少执行的次数，就需要未雨绸缪，每次扩充空间时，成倍增长。而每次执行的效率，就主要是数据移动的效率了。下面，我们依次介绍vector的数据结构，使用的空间配置器和迭代器，以及常用操作。 vector 的数据结构 vector的数据结构很简单，就是一段连续的物理空间，包含起止地址以及已用到的空间的末尾地址这三个成员：

template <class _Tp, class _Alloc>
class _Vector_base {
protected:
  _Tp* _M_start;
  _Tp* _M_finish;
  _Tp* _M_end_of_storage;
};
class vector : protected _Vector_base<_Tp, _Alloc>{
};

其中 _M_finish 是当前使用到的空间的结束地址，而 _M_end_of_storage 是可用空间的结束地址，前者小于等于后者，当新加入元素使得前者大于后者之后，就需要进行空间扩充了。

3. vector 的配置器

vector的空间配置器 STL 默认的 alloc 即 __default_alloc_template 配置器，即第二级配置器，它对于 POD(plain old data) 类型数据使用内建内存池来应对内存碎片问题，关于该默认配置器的更多介绍请参见本系列第2篇文章深入理解STL源码(1) 空间配置器 . 除此之外，SGI vector 还定义了一个 data_allocator，为的是更方便的以元素大小为配置单位：

template <class _Tp, class _Alloc>
class _Vector_base  // vector 继承了该基类
protected:
    typedef simple_alloc<_Tp, _Alloc> _M_data_allocator;
}

关于 simple_alloc 的内容见前面的文章，它其实就是简单的对 malloc 等的加一层封装。 vector的内存是在vector的构造或析构、插入元素而容量不够等情况下，需要进行配置。vector 提供了很多的构造函数，具体可见源代码，而更详细的列表并涉及各个版本的说明的列表可以参见C++的文档：cpp references.

4. vector 的迭代器

由于vector使用的物理连续的空间，需要支持随机访问，所以它使用的随机访问迭代器（Random Access Iterators）。也正由于vector使用连续物理空间，所以不论其元素类型为何，使用普通指针就可以作为它的迭代器：

public:
  typedef _Tp value_type;
  typedef value_type* iterator;
  typedef const value_type* const_iterator;

注意：vector中所谓的动态增加大小，并不是在原空间之后接连续新空间（因为无法保证原空间之后尚有可供配置的空间），而是以原大小的两倍另外配置一块较大空间，然后将原内容拷贝过来，然后再在其后构造新元素，最后释放原空间。因此，对于vector的任何操作，一旦引起空间重新配置，指向原vector的所有迭代器就失效了，这是vector使用中的一个大坑，务必小心。

5. vector 的常用操作

vector所提供的元素操作很多，这里选取几个常用操作介绍一下。 （1）push_back

public  void push_back(const _Tp& __x) {
if (_M_finish != _M_end_of_storage) {
    construct(_M_finish, __x);
    ++_M_finish;
}
else
    _M_insert_aux(end(), __x); // auxiliary insert
}

其中辅助的insert函数的基本逻辑为：按原空间大小的两倍申请新空间，复制原数据到新空间，释放原空间，更新新vector的数据结构的成员变量。 （2）insert

public  iterator insert(iterator __position, const _Tp& __x) {
    size_type __n = __position - begin();
    if (_M_finish != _M_end_of_storage && __position == end()) {
      construct(_M_finish, __x);
      ++_M_finish;
    }
    else
      _M_insert_aux(__position, __x);
    return begin() + __n;
  }

与push_back类似，只是push_back 在最后插入，更为简单。insert 首先判断是否为在最后插入且容量足够，如果是最后插入且容量足够就就直接内部实现了。否则还是调用上面的辅助插入函数，该函数中首先判断容量是否足够，容量足的话，先构造一个新元素并以当前vector的最后一个元素的值作为其初始值，然后从倒数第二个元素开始从后往前拷贝，将前一元素的值赋给后一元素，知道当前插入位置。 (3)erase

public  iterator erase(iterator __first, iterator __last) {
    iterator __i = copy(__last, _M_finish, __first);
    destroy(__i, _M_finish);
    _M_finish = _M_finish - (__last - __first);
    return __first;
  }

与insert相反，该函数将某些连续的元素从vector中删除，所以不存在容量不足等问题，但也不会将没有使用的空间归还给操作系统。这里只有简单的元素拷贝（copy）和元素的析构（destroy）。另外，需要说明的是，对于vector而言clear函数和erase函数是等同的，都只清空对应内存块的值，而不将空间归还给操作系统，所以vector的容量是只增不减的。而对于其他一些容器就有所不同了，比如list之类以node为单位的数据结构。关于vector的内容就介绍到这里了。

序列式容器之list

本文涉及到 SGI STL 源码的文件有list、stl_list.h、list.h 等几个文件。

1. list 和 slist

STL中也实现了链表这种数据结构，list是STL标准的双向链表，而slit是SGI的单链表。相比于vector的连续线性空间而言，list即有有点也有缺点：优点是空间分配更灵活，对任何位置的插入删除操作都是常数时间；缺点是排序不方便。list和vector是比较常用的线性容器，那么什么时候用哪一种容器呢，需要视元素的多少、元素构造的复杂度（是否为POD数据）以及元素存取行为的特性而定。限于篇幅，本文主要介绍list的内容，关于单链表slist可以参见源码和侯捷的书。

2. list 的数据结构

在数据结构中，我们知道链表的节点node和链表list本身是不同的数据结构，以下分别是node和list的数据结构：

struct _List_node_base {
  _List_node_base* _M_next;
  _List_node_base* _M_prev;
};
template <class _Tp>
struct _List_node : public _List_node_base {  // node 的定义
  _Tp _M_data;
};
template <class _Tp, class _Alloc>
class _List_base {
protected:
  _List_node<_Tp>* _M_node; // 只要一个指针就可以表示整个双向链表
};
template <class _Tp, class _Alloc = __STL_DEFAULT_ALLOCATOR(_Tp) >
class list : protected _List_base<_Tp, _Alloc> {
public:
  typedef _List_node<_Tp> _Node;
};

在list中的 _M_node 其实指向一个空白节点，该空白节点的 _M_data 成员是没有被初始化的，实际上该节点是链表的尾部，后面将list的迭代器还会提到这样做的好处。

3. list 的配置器

list缺省使用 alloc （即 __STL_DEFAULT_ALLOCATOR）作为空间配置器，并据此定义了另外一个 list_node_allocator ，并定义了_M_get_node和_M_put_node 两个函数，分别用于分配和释放空间，为的是更方便的以节点大小为配置单位。除此之外，还定义了两个_M_create_node 函数，在分配空间的同时调用元素的构建函数对其进行初始化：

template <class _Tp, class _Alloc>
class _List_base {
protected:
  typedef simple_alloc<_List_node<_Tp>, _Alloc> _Alloc_type; // 专属配置器，每次配置一个节点
  _List_node<_Tp>* _M_get_node() { return _Alloc_type::allocate(1); } // 分配一个节点
  void _M_put_node(_List_node<_Tp>* __p) { _Alloc_type::deallocate(__p, 1); }  // 释放一个节点
};
template <class _Tp, class _Alloc = __STL_DEFAULT_ALLOCATOR(_Tp) > // 缺省使用 __STL_DEFAULT_ALLOCATOR 配置器
class list : protected _List_base<_Tp, _Alloc> {
protected:
  _Node* _M_create_node(const _Tp& __x){ // 分配空间并初始化
    _Node* __p = _M_get_node();
    __STL_TRY {  _Construct(&__p->_M_data, __x);  }
    __STL_UNWIND(_M_put_node(__p));
    return __p;
  }
  _Node* _M_create_node(){
    _Node* __p = _M_get_node();
    __STL_TRY {  _Construct(&__p->_M_data);  }
    __STL_UNWIND(_M_put_node(__p));
    return __p;
  }
};

在list的构造和析构函数、插入、删除等操作中设计到空间的配置。由于list不涉及同时分配多个连续元素的空间，因此用不到SGI的第二层配置器。

4. list 的迭代器

由于list的节点在内存中不一定连续存储，其迭代器不能像vector那样使用普通指针了，由于list是双向的链表，迭代器必须具备前移、后移的能力，所以它的迭代器是BidirectionalIterators，即双向的可增可减的，以下是list的迭代器的设计：

struct _List_iterator_base {
  typedef bidirectional_iterator_tag iterator_category;
  _List_node_base* _M_node;
  _List_iterator_base(_List_node_base* __x) : _M_node(__x) {}
  _List_iterator_base() {}
  void _M_incr() { _M_node = _M_node->_M_next; }
  void _M_decr() { _M_node = _M_node->_M_prev; }
};
template<class _Tp, class _Ref, class _Ptr>
struct _List_iterator : public _List_iterator_base {
  _Self& operator++() { this->_M_incr(); return *this; }
  _Self operator++(int) { _Self __tmp = *this; this->_M_incr(); return __tmp; }
  _Self& operator--() { this->_M_decr(); return *this; }
  _Self operator--(int) { _Self __tmp = *this; this->_M_decr(); return __tmp; }
};

list有一个重要性质，插入操作（insert）和接合操作（splice）都不会造成原有list迭代器失效，而list的删除操作（erase）也只对“指向被删除元素”的那个迭代器失效，其他迭代器不受任何影响。

5. list 的常用操作

list的常用操作有很多，例如最基本的push_front、push_back、pop_front、pop_back 等，这里主要介绍一下clear、remove、unique、transfer 这几个。 （1）clear clear 函数的作用是清楚整个list的所有节点。

void clear() { _Base::clear(); }
void _List_base<_Tp,_Alloc>::clear() {
  _List_node<_Tp>* __cur = (_List_node<_Tp>*) _M_node->_M_next;
  while (__cur != _M_node) {
    _List_node<_Tp>* __tmp = __cur;
    __cur = (_List_node<_Tp>*) __cur->_M_next; // 后移
    _Destroy(&__tmp->_M_data); // 析构当前节点的对象
    _M_put_node(__tmp); // 释放当前节点的空间
  }
  _M_node->_M_next = _M_node; // 置为空list
  _M_node->_M_prev = _M_node;
}

（2）remove remove 函数的作用是将数值为value的所有元素移除。

void list<_Tp, _Alloc>::remove(const _Tp& __value) {
  iterator __first = begin();
  iterator __last = end();
  while (__first != __last) { // 遍历list
    iterator __next = __first;
    ++__next;
    if (*__first == __value) erase(__first); // 值与 value 相等就移除
    __first = __next;
  }
}

（3）unique unique函数的作用是移除相同的连续元素，只有“连续而且相同”的元素，才回被移除到只剩一个。

void list<_Tp, _Alloc>::unique() {
  iterator __first = begin();
  iterator __last = end();
  if (__first == __last) return;
  iterator __next = __first;
  while (++__next != __last) {
    if (*__first == *__next) // 连续连个节点的值相同
      erase(__next);
    else
      __first = __next;
    __next = __first;
  }
}

（4）transfer transfer的作用是将 [first, last) 内的所有元素移动到 position 之前。它是一个私有函数，它为其他常用操作如 splice、sort、merge 等的实现提供了便利。

protected:
  void transfer(iterator __position, iterator __first, iterator __last) {
    if (__position != __last) {
      // Remove [first, last) from its old position.
      __last._M_node->_M_prev->_M_next     = __position._M_node;
      __first._M_node->_M_prev->_M_next    = __last._M_node;
      __position._M_node->_M_prev->_M_next = __first._M_node;
      // Splice [first, last) into its new position.
      _List_node_base* __tmp      = __position._M_node->_M_prev;
      __position._M_node->_M_prev = __last._M_node->_M_prev;
      __last._M_node->_M_prev     = __first._M_node->_M_prev;
      __first._M_node->_M_prev    = __tmp;
    }
  }

关于list的内容就介绍到这里了。

序列式容器之deque和stack、queue

本文涉及到 SGI STL 源码的文件有deque、stl_deque.h、deque.h、stack、stl_stack.h、queue、stl_queue.h 等几个文件。

1. deque 概述

前面分别介绍了连续式存储的序列容器vector和以节点为单位链接起来的非连续存储的序列容器list，这两者各有优缺点，而且刚好是优缺互补的，那么何不将二者结合利用对方的优点来弥补己方的不足呢，于是这就有了强大的deque。

没错，与我们在数据结构中学到的固定连续空间的双端队列不同，STL中的deque是分段连续的空间通过list链接而成的序列容器，它结合了vector与list的存储特性，但与vector和list都不同的是deque只能在首部或尾部进行插入和删除操作，这个限制在一定程度上简化了deque实现的难度。由于使用分段连续空间链接的方式，所以deque不存在vector那样“因旧空间不足而重新配置新的更大的空间，然后复制元素，再释放原空间”的情形，也不会有list那样每次都只配置一个元素的空间而导致时间性能和空间的利用率低下。

2. deque 的数据结构

deque由一段一段连续空间串接而成，一旦有必要在deque的头部或尾端增加新的空间，便配置一段定量连续的空间，串接在deque的头部或尾端。deque的最大任务，就是在这些分段连续的空间上维护其整体连续的假象，并提供随机存取的接口。deque采用一块所谓的map（注意：不是STL中map容器，而是类似于vector）作为主控（为什么不使用list呢？），这块map是一个连续空间，其中每个元素都是一个指针，指向一段连续的空间，称为缓冲区，它才是deque的真正存储空间。SGI中允许指定缓冲区的大小，默认是512字节。除此之外，还有start和finish两个指针，分别指向第一个缓冲区的第一个元素和最后一个缓冲区的最后一个元素。其数据结构如下：

inline size_t __deque_buf_size(size_t __size) { // 计算缓冲区的大小
  return __size < 512 ? size_t(512 / __size) : size_t(1);
}
template <class _Tp, class _Alloc> class _Deque_base {
protected:
  _Tp** _M_map; // 指向缓冲区的指针数组首地址
  size_t _M_map_size;  // 指向缓冲区的指针数组的大小
  iterator _M_start; // 指向第一个缓冲区的第一个元素
  iterator _M_finish; // 指向最后一个缓冲区的最后一个元素
};
class deque : protected _Deque_base<_Tp, _Alloc> {
protected:  // Internal typedefs
  typedef pointer* _Map_pointer;
  static size_t _S_buffer_size() { return __deque_buf_size(sizeof(_Tp)); }
};

3. deque 的配置器

由于deque涉及到两种类型（map和buffer）数据的空间配置，因此deque定义了两个专属的配置器 _Map_alloc_type 和 _Node_alloc_type:

template <class _Tp, class _Alloc> class _Deque_base {
protected:
  typedef simple_alloc<_Tp, _Alloc>  _Node_alloc_type;
  typedef simple_alloc<_Tp*, _Alloc> _Map_alloc_type;
};
template <class _Tp, class _Alloc = __STL_DEFAULT_ALLOCATOR(_Tp) >
class deque : protected _Deque_base<_Tp, _Alloc> { };

而这里的 _Alloc 使用的都是STL默认的 alloc 这个配置器，因此这两个配置器实际上都是 alloc 类型的配置器，即SGI的第二级配置器。在定义一个deque时，默认调用基类的构造函数，产生一个map大小为0的空的deque，随着第一次插入元素，由于map大小不够，需要调用_M_push_back_aux 进而调用 _M_reallocate_map 进行map的空间配置，如果初始的map不为空，还需要对map进行“分配新空间，复制，释放元空间”的操作，如果从头部插入同样的道理，这是就是map的配置逻辑（实际中，还有一种情况，就是map的前后剩余的node数不同，例如前部分都空着，而后面插入后溢出了，这时可以考虑在map内部移动，即将后半部分整体往前移动一定距离）。其中_M_reallocate_map的实现如下：

template <class _Tp, class _Alloc>
void deque<_Tp,_Alloc>::_M_reallocate_map(size_type __nodes_to_add, bool __add_at_front){
  size_type __old_num_nodes = _M_finish._M_node - _M_start._M_node + 1;
  size_type __new_num_nodes = __old_num_nodes + __nodes_to_add;
  _Map_pointer __new_nstart;
  if (_M_map_size > 2 * __new_num_nodes) { // map的size足够，在map内部移动
    __new_nstart = _M_map + (_M_map_size - __new_num_nodes) / 2 + (__add_at_front ? __nodes_to_add : 0);
    if (__new_nstart < _M_start._M_node)
      copy(_M_start._M_node, _M_finish._M_node + 1, __new_nstart);
    else
      copy_backward(_M_start._M_node, _M_finish._M_node + 1, __new_nstart + __old_num_nodes);
  } else { // map的size不够，重新分配
    size_type __new_map_size = _M_map_size + max(_M_map_size, __nodes_to_add) + 2;
    _Map_pointer __new_map = _M_allocate_map(__new_map_size); // 重新分配map
    __new_nstart = __new_map + (__new_map_size - __new_num_nodes) / 2 + (__add_at_front ? __nodes_to_add : 0);
    copy(_M_start._M_node, _M_finish._M_node + 1, __new_nstart); // 复制原map到新的map中
    _M_deallocate_map(_M_map, _M_map_size); // 释放原map
    _M_map = __new_map;
    _M_map_size = __new_map_size;
  }
  _M_start._M_set_node(__new_nstart);
  _M_finish._M_set_node(__new_nstart + __old_num_nodes - 1);
}

那么每个连续的缓冲区buffer（或node）是在什么时候配置呢？它是在map中实际使用到的最后一个node不够用时但map还可以继续在这个node后面加入node时（即map非满而node满时），在 _M_push_back_aux 中调用 _M_allocate_node 来分配，相关函数都比较简单，这里就不贴了。以上主要是空间分配相关的，那么在 pop 的时候，空间的释放又是怎样的呢？这里也需要判断是否当前node全部被 pop 了，如果是的则需要释放这个node所占用的空间。如下：

void pop_back() { // deque内部实现的成员函数，inline的
    if (_M_finish._M_cur != _M_finish._M_first) { // 整个node还没有pop完
      --_M_finish._M_cur;
      destroy(_M_finish._M_cur); // 析构当前元素
    } else  _M_pop_back_aux();
}
template <class _Tp, class _Alloc>
void deque<_Tp,_Alloc>::_M_pop_back_aux() { // 整个node被pop完了的情况
  _M_deallocate_node(_M_finish._M_first); // 释放整个node的空间
  _M_finish._M_set_node(_M_finish._M_node - 1); // node前移
  _M_finish._M_cur = _M_finish._M_last - 1; // 当前元素为最后一个node的最后一个元素
  destroy(_M_finish._M_cur); // 释放当前元素
}

4. deque 的迭代器

deque是分段连续空间，前面也提到了deque使用的是Bidirectional Iterators，因此deque的迭代器主要需要实现operator++和operator--。要实现这两个操作，需要考虑当前指针是否处于buffer的头/尾，如果在buffer的头部而需要前移（或尾部需要后移），就需要将buffer往前/后移一个，在SGI中是通过调用 _M_set_node 来实现的。具体代码如下：

template <class _Tp, class _Ref, class _Ptr> struct _Deque_iterator {
  typedef _Tp** _Map_pointer;
  _Tp* _M_cur; // 几个成员变量
  _Tp* _M_first;
  _Tp* _M_last;
  _Map_pointer _M_node;
  _Self& operator++() { // ++ 操作符重载，后移
    ++_M_cur;
    if (_M_cur == _M_last) { // 到了buffer的最后一个
      _M_set_node(_M_node + 1); // 将当前node指针_M_node指向下一个node
      _M_cur = _M_first; // 当前指针指向新node的第一个元素
    }
    return *this;
  }
  void _M_set_node(_Map_pointer __new_node) {
    _M_node = __new_node; // map pointer后移
    _M_first = *__new_node; // first指向新node
    _M_last = _M_first + difference_type(_S_buffer_size()); // last指向下一个node
  }
};

使用 -- 操作符向前移动的同理，这里就不赘述了。

5. deque 的常用操作

deque中最常用的莫过于 push 和 pop 操作了，这些操作在前面的空间配置中基本已经介绍了，这里就主要介绍一下 clear、 erase 和 insert 操作吧。 （1）clear 该函数的作用是清除整个deque，释放所有空间而只保留一个缓冲区：

template <class _Tp, class _Alloc> void deque<_Tp,_Alloc>::clear() {
  for (_Map_pointer __node = _M_start._M_node + 1; __node < _M_finish._M_node; ++__node) { // 从第二个node开始，遍历每个缓冲区（node）
    destroy(*__node, *__node + _S_buffer_size()); // 析构每个元素
    _M_deallocate_node(*__node); // 释放缓冲区
  }
  if (_M_start._M_node != _M_finish._M_node) { // 还剩下头尾两个node
    destroy(_M_start._M_cur, _M_start._M_last); // 析构头node中的每个元素
    destroy(_M_finish._M_first, _M_finish._M_cur); // 析构尾node中的每个元素
    _M_deallocate_node(_M_finish._M_first); // 释放尾node的空间
  } else destroy(_M_start._M_cur, _M_finish._M_cur); // 只有一个node，析构这个node中的所有元素
  _M_finish = _M_start;
}

（2）erase 该函数的作用是清除 [first,last) 间的所有元素：

typename deque<_Tp,_Alloc>::iterator
deque<_Tp,_Alloc>::erase(iterator __first, iterator __last) {
  if (__first == _M_start && __last == _M_finish) { // erase 所有元素，直接调用clear
    clear();
    return _M_finish;
  } else { // erase 部分元素
    difference_type __n = __last - __first; // 待擦出的区间长度
    difference_type __elems_before = __first - _M_start; // 擦出区间前的元素个数
    if (__elems_before < difference_type((this->size() - __n) / 2)) { // 前面的元素个个数小于擦除后剩余总数的一半，将这部分后移
      copy_backward(_M_start, __first, __last); // 后移
      iterator __new_start = _M_start + __n;
      destroy(_M_start, __new_start);
      _M_destroy_nodes(__new_start._M_node, _M_start._M_node);
      _M_start = __new_start;
    } else { // 前面剩余的元素较多，将后面的前移
      copy(__last, _M_finish, __first); // 前移
      iterator __new_finish = _M_finish - __n;
      destroy(__new_finish, _M_finish);
      _M_destroy_nodes(__new_finish._M_node + 1, _M_finish._M_node + 1);
      _M_finish = __new_finish;
    }
    return _M_start + __elems_before;
  }
}

（3）insert 该函数的作用是在某个位置插入一个元素：

iterator insert(iterator position, const value_type& __x) {
  if (position._M_cur == _M_start._M_cur) { // 在头部插入，用push_front
    push_front(__x);
    return _M_start;
  } else if (position._M_cur == _M_finish._M_cur) { // 在尾部插入
    push_back(__x);
    iterator __tmp = _M_finish;
    --__tmp;
    return __tmp; // 返回插入位置
  } else { // 在中间插入
    return _M_insert_aux(position, __x);
  }
}
deque<_Tp,_Alloc>::_M_insert_aux(iterator __pos, const value_type& __x) {
  difference_type __index = __pos - _M_start; // 插入点之前的元素个数
  value_type __x_copy = __x;
  if (size_type(__index) < this->size() / 2) { // 前面的元素个数较小
    push_front(front()); // 在头部插入与头部相同的元素，然后从第二个元素开始到插入位置整体前移一步
    iterator __front1 = _M_start; ++__front1;
    iterator __front2 = __front1; ++__front2;
    __pos = _M_start + __index;
    iterator __pos1 = __pos; ++__pos1;
    copy(__front2, __pos1, __front1);
  } else { // 插入点后面的元素较少，从后面插入，然后插入点到尾部整体往后移一步
    push_back(back());
    iterator __back1 = _M_finish; --__back1;
    iterator __back2 = __back1;  --__back2;
    __pos = _M_start + __index;
    copy_backward(__pos, __back2, __back1);
  }
  *__pos = __x_copy;
  return __pos;
}

deque原本只能在头部或尾部插入元素的，提供了insert之后，就可以任何位置插入元素了。

6. 基于deque 的 stack 和 queue

由于deque可以从首位两端插入或剔除元素，所以只需要对其进行简单的封装就可以分别实现先进先出（FIFO）的stack和先进后出（FILO）的queue了。stack和queue中都有一个deque类型的成员，用做数据存储的容器，然后对deque的部分接口进行简单的封装，例如stack只提供从末端插入和删除的接口以及获取末端元素的接口，而queue则只提供从尾部插入而从头部删除的接口以及获取首位元素的接口。像这样具有“修改某物接口，形成另一种风貌”的性质的，称为配接器（adapter），因此STL中stack和queue往往不被归类为容器（container），而被归类为容器配接器（container adapter）。（关于配接器后面文章还会具体介绍）下面只给出stack的基本实现，并加以注解。

template <class _Tp, class _Sequence __STL_DEPENDENT_DEFAULT_TMPL(deque<_Tp>) >
class stack; // 原型声明
template <class _Tp, class _Sequence> class stack {
protected:
  _Sequence c; // _Sequence为deque<_Tp>，c为实际存储数据的容器
public: // 向外部提供的接口，都是调用deque的接口来实现的
  stack() : c() {}
  explicit stack(const _Sequence& __s) : c(__s) {}
  bool empty() const { return c.empty(); }
  size_type size() const { return c.size(); }
  reference top() { return c.back(); }
  const_reference top() const { return c.back(); }
  void push(const value_type& __x) { c.push_back(__x); }
  void pop() { c.pop_back(); }
};

值得一提的是，stack和queue都没有迭代器，因此不能对stack或queue进行遍历。但他们提供了 operator == 和 operator< 这两个比较大小的操作符：

template <class _Tp, class _Seq>
bool operator==(const stack<_Tp,_Seq>& __x, const stack<_Tp,_Seq>& __y) {
  return __x.c == __y.c;
}
template <class _Tp, class _Seq>
bool operator<(const stack<_Tp,_Seq>& __x, const stack<_Tp,_Seq>& __y) {
  return __x.c < __y.c;
}

另外，除了使用默认的deque作为stack和queue的容器之外，我们还可以使用list或其他自定义的容器，只需要实现了stack或queue需要的接口，使用方法很简单：

stack<int,vector<int> > ist;
queue<char,list<char> > cq;

即只需要指定模板中第二个参数即可。关于deque的内容就介绍到这里了。

序列式容器之heap和priority Queue

本文涉及到 SGI STL 源码的文件有heap、stl_heap.h、heap.h、stl_queue.h、queue 等几个文件。

1. 概述

前面分别介绍了三种各具特色的序列式容器 —— vector、list和deque，他们几乎可以涵盖所有类型的序列式容器了，但本文要介绍的heap则是一种比较特殊的容器。其实，在STL中heap并没有被定义为一个容器，而只是一组算法，提供给priority queue（优先队列）。故名思议，priority queue 允许用户以任何次序将元素放入容器内，但取出时一定是从优先权最高的元素开始取，binary max heap（二元大根堆）即具有这样的特性，因此如果学过max-heap再看STL中heap的算法和priority queue 的实现就会比较简单。

2. priority queue 的数据结构

要实现priority queue的功能，binary search tree（BST）也可以作为其底层机制，但这样的话元素的插入就需要O(logN)的平均复杂度，而且要求元素的大小比较随机，才能使树比较平衡。而binary heap是一种完全二叉树的结构，而且可以使用vector来存储：

template <class _Tp, class _Sequence __STL_DEPENDENT_DEFAULT_TMPL(vector<_Tp>),
          class _Compare __STL_DEPENDENT_DEFAULT_TMPL(less<typename _Sequence::value_type>) >
class priority_queue { // in stl_queue.h 文件中
protected:
  _Sequence c; // 使用vector作为数据存储的容器
  _Compare comp;
};

另外只需要提供一组heap算法，即元素插入和删除、获取堆顶元素等操作即可。

3. push heap 算法

为了满足完全二叉树的特性，新加入的元素一定要放在vector的最后面；又为了满足max-heap的条件（每个节点的键值不小于其叶子节点的键值），还需要执行上溯过程，将新插入的元素与其父节点进行比较，直到不大于父节点：

template <class _RandomAccessIterator, class _Distance, class _Tp>
void __push_heap(_RandomAccessIterator __first, _Distance __holeIndex, _Distance __topIndex, _Tp __value){
  _Distance __parent = (__holeIndex - 1) / 2; //  新节点的父节点
  while (__holeIndex > __topIndex && *(__first + __parent) < __value) { // 插入时的堆调整过程：当尚未到达顶端且父节点小于新值时，需要将新值往上（前）调整
    *(__first + __holeIndex) = *(__first + __parent); // 父节点下移
    __holeIndex = __parent;
    __parent = (__holeIndex - 1) / 2;
  }
  *(__first + __holeIndex) = __value; // 找到新值应当存储的位置
}
template <class _RandomAccessIterator, class _Distance, class _Tp>
inline void __push_heap_aux(_RandomAccessIterator __first, _RandomAccessIterator __last, _Distance*, _Tp*) {
  __push_heap(__first, _Distance((__last - __first) - 1), _Distance(0), _Tp(*(__last - 1)));
}
template <class _RandomAccessIterator>
inline void push_heap(_RandomAccessIterator __first, _RandomAccessIterator __last) { // 真正的对外接口，在调用之前，元素已经放在了vector的最后面了（见priority queue的push_back）
  __STL_REQUIRES(_RandomAccessIterator, _Mutable_RandomAccessIterator);
  __STL_REQUIRES(typename iterator_traits<_RandomAccessIterator>::value_type, _LessThanComparable);
  __push_heap_aux(__first, __last, __DISTANCE_TYPE(__first), __VALUE_TYPE(__first)); // 直接调用 __push_heap_aux
}

4. pop heap 算法

对heap进行pop操作就是取顶部的元素，取走后要对heap进行调整，是之满足max-heap的特性。调整的策略是，首先将最末尾的元素放到堆顶，然后进行下溯操作，将对顶元素下移到适当的位置：

template <class _RandomAccessIterator, class _Distance, class _Tp>
void __adjust_heap(_RandomAccessIterator __first, _Distance __holeIndex, _Distance __len, _Tp __value) { // 调整堆
  _Distance __topIndex = __holeIndex; // 堆顶
  _Distance __secondChild = 2 * __holeIndex + 2;
  while (__secondChild < __len) {
    if (*(__first + __secondChild) < *(__first + (__secondChild - 1))) __secondChild--; // secondChild 为左右两个子节点中较大者
    *(__first + __holeIndex) = *(__first + __secondChild); // 节点的值上移
    __holeIndex = __secondChild;
    __secondChild = 2 * (__secondChild + 1); // 下移一层
  }
  if (__secondChild == __len) { // 最后一个元素
    *(__first + __holeIndex) = *(__first + (__secondChild - 1));
    __holeIndex = __secondChild - 1;
  }
  __push_heap(__first, __holeIndex, __topIndex, __value);
}
template <class _RandomAccessIterator, class _Tp, class _Distance>
inline void __pop_heap(_RandomAccessIterator __first, _RandomAccessIterator __last, _RandomAccessIterator __result, _Tp __value, _Distance*) {
  *__result = *__first; // 获取堆顶元素，并赋给堆尾的last-1
  __adjust_heap(__first, _Distance(0), _Distance(__last - __first), __value); // 调整堆
}
template <class _RandomAccessIterator, class _Tp>
inline void __pop_heap_aux(_RandomAccessIterator __first, _RandomAccessIterator __last, _Tp*) {
  __pop_heap(__first, __last - 1, __last - 1, _Tp(*(__last - 1)), __DISTANCE_TYPE(__first)); // 对 [first,last-1)进行pop，并将first赋给last-1
}
template <class _RandomAccessIterator>
inline void pop_heap(_RandomAccessIterator __first, _RandomAccessIterator __last) { // 对外提供的接口，最后堆顶元素在堆的末尾，而[first,last-1) 区间为新堆，该接口调用完后再进行pop操作移除最后的元素
  __STL_REQUIRES(_RandomAccessIterator, _Mutable_RandomAccessIterator);
  __STL_REQUIRES(typename iterator_traits<_RandomAccessIterator>::value_type, _LessThanComparable);
  __pop_heap_aux(__first, __last, __VALUE_TYPE(__first));
}

5. make heap 算法

最后，我们来看看如何从一个初始序列来创建一个heap，有了前面的 adjust_heap ，创建heap也就很简单了，只需要从最后一个非叶子节点开始，不断调用堆调整函数，即可使得整个序列称为一个heap：

template <class _RandomAccessIterator, class _Compare, class _Tp, class _Distance>
void __make_heap(_RandomAccessIterator __first, _RandomAccessIterator __last, _Compare __comp, _Tp*, _Distance*) {
  if (__last - __first < 2) return;
  _Distance __len = __last - __first;
  _Distance __parent = (__len - 2)/2; // 定位到最后一个非叶子节点
  while (true) { // 对每个非叶子节点为根的子树进行堆调整
    __adjust_heap(__first, __parent, __len, _Tp(*(__first + __parent)), __comp);
    if (__parent == 0) return;
    __parent--;
  }
}
template <class _RandomAccessIterator, class _Compare>
inline void make_heap(_RandomAccessIterator __first, _RandomAccessIterator __last, _Compare __comp) { // 对外提供的接口
  __STL_REQUIRES(_RandomAccessIterator, _Mutable_RandomAccessIterator);
  __make_heap(__first, __last, __comp, __VALUE_TYPE(__first), __DISTANCE_TYPE(__first));
}

6. 基于 heap 的 priority queue

上一篇文章中讲到stack和queue都是基于deque实现的，这里的priority queue是基于vector和heap来实现的，默认使用vector作为容器，而使用heap的算法来维持其priority的特性，因此priority queue也被归类为container adapter。其具体实现的主要代码如下:

template <class _Tp, class _Sequence __STL_DEPENDENT_DEFAULT_TMPL(vector<_Tp>), class _Compare __STL_DEPENDENT_DEFAULT_TMPL(less<typename _Sequence::value_type>) >
class priority_queue {
protected:
  _Sequence c;
  _Compare comp;
public:
  priority_queue() : c() {}
  explicit priority_queue(const _Compare& __x) :  c(), comp(__x) {}
  priority_queue(const _Compare& __x, const _Sequence& __s) : c(__s), comp(__x)
    { make_heap(c.begin(), c.end(), comp); }
  bool empty() const { return c.empty(); }
  size_type size() const { return c.size(); }
  const_reference top() const { return c.front(); }
  void push(const value_type& __x) {
    __STL_TRY {
      c.push_back(__x); // 在push_heap之前先将x放在vector c的最后面
      push_heap(c.begin(), c.end(), comp);
    }
    __STL_UNWIND(c.clear());
  }
  void pop() {
    __STL_TRY {
      pop_heap(c.begin(), c.end(), comp);
      c.pop_back(); // 在调用pop_heap之后才将最后一个元素剔除出vector c
    }
    __STL_UNWIND(c.clear());
  }
};

值得一提的是，priority queue也没有迭代器，不能对其进行遍历等操作，因为它只能在顶部取和删除元素，而插入元素的位置也是确定的，而不能有用户指定。关于heap和priority queue的内容就介绍到这里了，而序列式容器的介绍也到此结束了。

关联式容器之红黑树

本文涉及到 SGI STL 源码的文件主要是 stl_tree.h 这个文件。

0. 关联式容器

之前几篇文章详细介绍了SGI STL中序列式容器的实现，并提到过STL中还有一类关联式的容器。标准的STL管理师容器分为 set（集合）和map（映射表）两大类，以及这两大类的衍生体multiset（多键集合）和multimap（多键映射表），这些容器的底层机制均以RB-Tree（红黑树）完成。RB-Tree是一种非常高效的数据结构，它本质上是一种平衡的二叉搜索树，因而其查找的平均时间复杂度为元素总个数的对数（即logN）。在STL中RB-Tree是一个独立的容器，但并没有对用户的公开接口，仅提供给STL的set和map使用。 SGI STL在标准STL之外，还提供了一类关联式容器——hash table（哈希表），以及以此为低层机制的hash set（散列集合）、hash map（散列映射表）、hash multiset（散列多键集合）和hash multimap（散列多键映射表）。相比于RB-Tree，hash table的时间效率更高，插入、删除、查找的时间复杂度均为常数时间，但需要比元素总个数多得多的空间。本文接下来主要介绍树及RB-Tree相关的内容，后续文章将具体介绍SGI STL中set、map、hash table的实现。

1. 树与二叉搜索树

树是一种非常常见而且实用的数据结构，几乎所有的操作系统都将文件存放在树状结构里，几乎所有编译器需要实现一个表达式树（expression tree），文件压缩所用的哈夫曼算法也需要用到树状结构，数据库所使用的B-tree则是一种相当复杂的树状结构。关于树的一些基本概念相信大家都比较熟悉，这里就不赘述了，如果需要可以google或看wikipedia，这里重点重温一下数据结构里的二叉搜索树、平衡二叉搜索树、AVL树。 二叉搜索树：任何节点的键值大于其左子树中每一个节点的键值，并小于其右子树中的每一个节点的键值。根据二叉搜索树的定义可知，按照中序遍历该树可以得到一个有序的序列。平均情况下，二叉搜索树可以提供对数时间的插入和访问。其插入和查找的算法也很简单，每次与根节点的键值进行比较，小于根节点的键值则往根节点的左子树插入或查找，大于则往右子树插入或查找，无论是递归实现还是非递归实现都很简单。 平衡二叉搜索树：上面提到二叉搜索数的平均性能为对数时间，这是因为二叉搜索树的深度与数据插入的顺序有关，如果插入的数据本身就比较有序，那么就会产生一个深度过大的树，甚至会退化为一个链表的结构，这中情况下，其查找的效率就是线性时间了。平衡二叉搜索树就是为了解决这个问题而产生的，“平衡”的意义是，没有任何一个节点过深。不同的平衡条件造就出不同的效率表现，以及不同的实现复杂度，如 AVL-Tree、RB-Tree、AA-Tree _等。他们都比简单的二叉搜索树要复杂，特别是插入和删除操作，但他们可以避免高度不平衡的情况，因而查找时间较快。

AVL树：AVL-tree（Adelson-Velskii-Landis tree）是一个加上了“额外平衡条件”的二叉搜索树，是一种高度平衡的二叉搜索树，它的这个额外的条件为：任何节点的左右子树高度相差最多1。该条件能够保证整棵树的高度为logN，但其插入和删除的操作也相对比较复杂，因为这些操作可能导致树的失衡，需要调整（或旋转）树的结构，使其保持平衡。插入时出现失衡的情况有如下四种（其中X为最小失衡子树的根节点）：

插入点位于X的左子节点的左子树——左左；

插入点位于X的左子节点的右子树——左右；

插入点位于X的右子节点的左子树——右左；

插入点位于X的右子节点的右子树——右右。

情况1和4对称，称为外侧插入，可以采用单旋转操作调整恢复平衡；2和3对称，称为内侧插入，可以采用双旋转操作调整恢复平衡：先经过一次旋转变成左左或右右，然后再经过一次旋转恢复平衡。1和2的实例如下图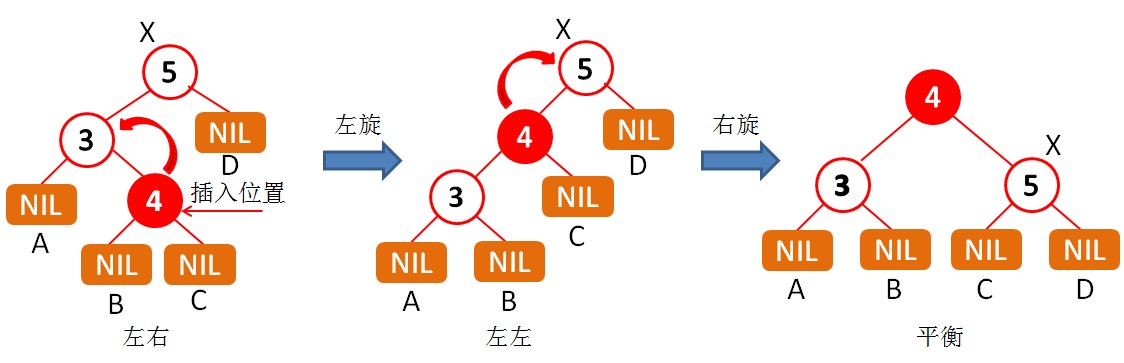：图中从中间到最右情况1的恢复平衡的旋转方法，只是其中节点3为新插入的元素；而最左到最右是情况2的恢复平衡的旋转方法，其中节点4为新插入的元素。情况3和4分别与2和1对称，其调整方法也很类似，就不赘述了。 RB-tree是另一种被广泛使用的平衡二叉搜索树，也是SGI STL唯一实现的一种搜索树，作为关联式容器的底层容器。RB-tree的平衡条件不同于AVL-tree，但同样运用了单旋转和双旋转的恢复平衡的机制，下面我们详细介绍RB-tree的实现。

2. RB-tree的定义及数据结构

所谓RB-tree，不仅仅是一个二叉搜索树，而且必须满足以下规则：

每个节点不是红色就是黑色；

根节点为黑色；

每个叶子节点（NIL）为黑色；

如果节点为红，其左右子节点必为黑；

对每个节点，从该节点到其子孙中的叶子节点的所有路径上所包含的黑节点数目相同。

上面的这些约束保证了这个树大致上是平衡的，这也决定了红黑树的插入、删除、查询等操作是比较快速的。根据规则5，新增节点必须为红色；根据规则4，新增节点之父节点必须为黑色。当新增节点根据二叉搜索树的规则到达其插入点时，却未能符合上述条件时，就必须调整颜色并旋转树形。下图是一个典型的RB-tree（来自wiki）： SGI STL中RB-tree的数据结构比较简单，其中每个节点的数据结构如下：

typedef bool _Rb_tree_Color_type;
const _Rb_tree_Color_type _S_rb_tree_red = false;
const _Rb_tree_Color_type _S_rb_tree_black = true;
//======================================
struct _Rb_tree_node_base { // 节点的定义
  typedef _Rb_tree_Color_type _Color_type;
  typedef _Rb_tree_node_base* _Base_ptr;
  _Color_type _M_color; // 节点颜色，实际为一个bool型变量
  _Base_ptr _M_parent; // 指向父节点，方便遍历
  _Base_ptr _M_left;
  _Base_ptr _M_right;

  static _Base_ptr _S_minimum(_Base_ptr __x) {
    while (__x->_M_left != 0) __x = __x->_M_left;
    return __x;
  }
  static _Base_ptr _S_maximum(_Base_ptr __x) {
    while (__x->_M_right != 0) __x = __x->_M_right;
    return __x;
  }
};
//======================================
template <class _Value> struct _Rb_tree_node : public _Rb_tree_node_base { // 节点的定义
  typedef _Rb_tree_node<_Value>* _Link_type;
  _Value _M_value_field;
};

其中每个节点主要包含一个标志颜色的bool变量 _M_color，3个节点指针 _M_parent , _M_left , _M_right，2个成员函数 _S_minimum 和 _S_maximum （分别求取最小（最左）、最大（最右）节点）。而RB-tree的定义如下：

template <class _Tp, class _Alloc> struct _Rb_tree_base { // RB-tree的定义
  typedef _Alloc allocator_type;
  allocator_type get_allocator() const { return allocator_type(); }
  _Rb_tree_base(const allocator_type&)  : _M_header(0) { _M_header = _M_get_node(); } // 构造函数
  ~_Rb_tree_base() { _M_put_node(_M_header); } // 析构函数
protected:
  _Rb_tree_node<_Tp>* _M_header; // 根节点
  typedef simple_alloc<_Rb_tree_node<_Tp>, _Alloc> _Alloc_type; // 空间配置器
  _Rb_tree_node<_Tp>* _M_get_node()  { return _Alloc_type::allocate(1); } // 分配一个节点的空间
  void _M_put_node(_Rb_tree_node<_Tp>* __p) { _Alloc_type::deallocate(__p, 1); } // 释放__p节点的空间
};
//======================================
template <class _Key, class _Value, class _KeyOfValue, class _Compare,
          class _Alloc = __STL_DEFAULT_ALLOCATOR(_Value) >
class _Rb_tree : protected _Rb_tree_base<_Value, _Alloc> {
  typedef _Rb_tree_base<_Value, _Alloc> _Base;
// ... 
};

可以看到RB-tree的空间配置器是 simple_alloc 配置器，按 _Rb_tree_node 节点大小分配空间，每次分配或释放一个节点的空间。

3. RB-tree的迭代器

要将RB-tree实现为一个泛型容器并用作set、map的低层容器，迭代器的设计是一个关键。RB-tree的迭代器是一个双向迭代器，但不具备随机访问能力，其引用（dereference）和访问（access）操作与list十分类似，较为特殊的是自增（operator++）和自减（operator–）操作，这里的自增/自减操作是指将迭代器移动到RB-tree按键值大小排序后当前节点的下一个/上一个节点，也即按中序遍历RB-tree时当前节点的下一个/上一个节点。RB-tree的迭代器的定义如下：

struct _Rb_tree_base_iterator {
  typedef _Rb_tree_node_base::_Base_ptr _Base_ptr;
  typedef bidirectional_iterator_tag iterator_category;
  void _M_increment()  { }
  void _M_decrement()  { }
};
template <class _Value, class _Ref, class _Ptr>
struct _Rb_tree_iterator : public _Rb_tree_base_iterator {
  _Self& operator++() { _M_increment(); return *this; }
  _Self& operator--() { _M_decrement(); return *this; }
};

可以看到RB-tree的自增和自减操作是使用基迭代器的increment和decrement来实现的，这里仅分析自增操作的实现（自减操作类似的）。RB-tree的自增操作实际上是寻找中序遍历下当前节点的后一个节点，其代码如下：

  void _M_increment()  { // 自增操作，中序遍历的下一个节点
    if (_M_node->_M_right != 0) { // 当前节点有右子树
      _M_node = _M_node->_M_right;
      while (_M_node->_M_left != 0) // 右子树的最左节点即为所求
        _M_node = _M_node->_M_left;
    } else { // 当前节点没有右子树，找父节点且父节点的右子树不包含当前节点的祖先节点
      _Base_ptr __y = _M_node->_M_parent;
      while (_M_node == __y->_M_right) { // 当前节点在父节点的右子树中就继续往父节点的父节点找
        _M_node = __y;
        __y = __y->_M_parent;
      }
      if (_M_node->_M_right != __y)
        _M_node = __y;
    }
  }

下面几节主要介绍一下RB-tree的基本操作。

4. RB-tree的插入操作

4.1 基本插入操作

RB-tree提供两种插入操作，insert_unique() 和 insert_equal()，顾名思义，前者表示被插入的节点的键值在树中是唯一的（如果已经存在，就不需要插入了），后者表示可以存在键值相同的节点。这两个函数都有多个版本，下面以后者的最简单版本（单一参数：被插入的节点的键值）为实例进行介绍。下面是 insert_equal 的实现：

_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc> ::insert_equal(const _Value& __v) {
  _Link_type __y = _M_header;
  _Link_type __x = _M_root(); // 从根节点开始
  while (__x != 0) { // 往下寻找插入点
    __y = __x;
    // 比较，当前节点的键值比插入值大往左子树找，否则往右子树找
    __x = _M_key_compare(_KeyOfValue()(__v), _S_key(__x)) ? _S_left(__x) : _S_right(__x);
  }
  return _M_insert(__x, __y, __v); // 真正的插入操作，x为新插入节点，y为x的父节点，v为新值
}
//真正的插入操作，主要是对RB-tree及新节点的成员变量的设置
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc> ::_M_insert(_Base_ptr __x_, _Base_ptr __y_, const _Value& __v) {
  _Link_type __x = (_Link_type) __x_;
  _Link_type __y = (_Link_type) __y_;
  _Link_type __z;
  if (__y == _M_header || __x != 0 || _M_key_compare(_KeyOfValue()(__v), _S_key(__y))) {
    __z = _M_create_node(__v); // 创建新节点
    _S_left(__y) = __z;     // makes _M_leftmost() = __z, when __y == _M_header
    if (__y == _M_header) { // y为header
      _M_root() = __z;
      _M_rightmost() = __z;
    } else if (__y == _M_leftmost()) // y为最左节点
      _M_leftmost() = __z;  // maintain _M_leftmost() pointing to min node
  } else {
    __z = _M_create_node(__v); // 创建新节点。???为什么不放到if-else上面???
    _S_right(__y) = __z; // 新节点为y的右孩子
    if (__y == _M_rightmost()) // y为最右节点
      _M_rightmost() = __z; // maintain _M_rightmost() pointing to max node
  }
  _S_parent(__z) = __y; // 设定新节点的父节点
  _S_left(__z) = 0;
  _S_right(__z) = 0;
  _Rb_tree_rebalance(__z, _M_header->_M_parent); // 调整RB-tree使之恢复平衡
  ++_M_node_count;
  return iterator(__z); // 返回指向新节点的迭代器
}

至此新节点插入完成。然而，由于新节点的插入，可能会引起RB-tree的性质4,5的破坏，需要对RB-tree进行旋转并对相关节点重新着色，这都是在 _Rb_tree_rebalance 这个函数中实现的，下面就主要介绍RB-tree是如何恢复平衡。

4.2 调整RB-tree使之恢复平衡

RB-tree的调整与AVL-tree类似但更复杂，因为不仅仅需要旋转，还需要考虑节点的颜色是否符合要求。破坏RB-tree性质4的可能起因是插入了一个红色节点、将一个黑色节点变为红色或者是旋转，而破坏性质5的可能原因是插入一个黑色的节点、节点颜色的改变（红变黑或黑变红）或者是旋转。在讨论 RB-tree 插入操作之前必须明白一点，那就是新插入的节点的颜色必为红色（调整前），因为插入黑点会增加某条路径上黑结点的数目，从而导致整棵树黑高度的不平衡。但如果新结点的父结点为红色时（如下图所示），将会违反红黑树的性质：一条路径上不能出现父子同为红色结点。这时就需要通过一系列操作来使红黑树保持平衡。为了清楚地表示插入操作以下在结点中使用“N”字表示一个新插入的结点，使用“P”字表示新插入点的父结点，使用“U”字表示“P”结点的兄弟结点，使用“G”字表示“P”结点的父结点。插入操作分为以下几种情况： 1）、树为空 此时，新插入节点为根节点，上面说过新插入节点均为红色，这不符合RB-tree的性质2，只需要将新节点重新改为黑色即可。 2）、黑父 如果新节点的父结点为黑色结点，那么插入一个红点将不会影响红黑树的平衡，此时插入操作完成。红黑树比AVL树优秀的地方之一在于黑父的情况比较常见，从而使红黑树需要旋转的几率相对AVL树来说会少一些。 3）、红父 这种情况就比较复杂。由于父节点为红，所以祖父节点必为黑色。由于新节点和父节点均为红，所以需要重新着色或进行旋转，此时就需要考虑叔父节点的颜色，进而可能需要考虑祖父、祖先节点的颜色。 3.1）、叔父为红 只要将父和叔结点变为黑色，将祖父结点变为红色即可，如下图所示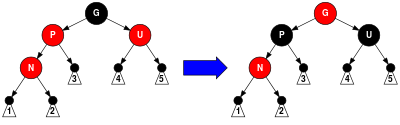：但由于祖父结点的父结点有可能为红色，从而违反红黑树性质。此时必须将祖父结点作为新的判定点继续向上（迭代）进行平衡操作。 3.2）、叔父为黑 当叔父结点为黑色时，需要进行旋转，有4中情况（类似AVL），以下图示了所有的旋转可能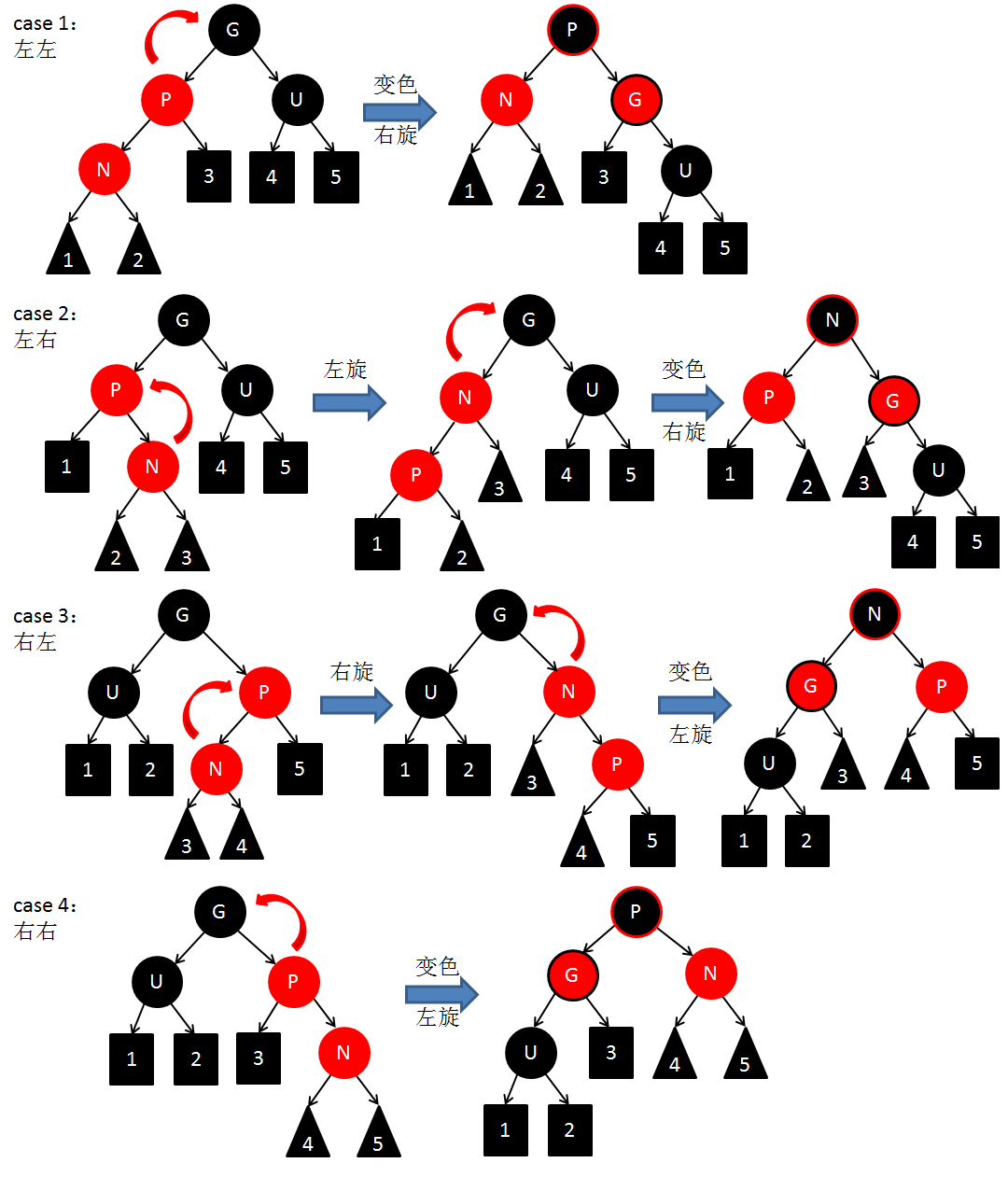：可以观察到，当旋转完成后，新的旋转根全部为黑色，此时不需要再向上回溯进行平衡操作，插入操作完成。篇幅原因，相关代码这里就不粘贴出来了，要注意的一点就是case1和case2的变色方案是一样的，虽然从上图中看一个是P由红变黑，一个是N由红变黑，但实际上在case2中，经过一次旋转后，迭代器所指向的节点已经发生改变，这样刚好使得这两个case的变色方案相同，均为P由红变黑而G由黑变红。case3与case4的变色方案也是类似的。

5. RB-tree的删除操作

相比于插入操作，RB-tree的删除操作更加复杂。在侯捷的书上并没有讲删除操作，而在算法导论上是有专门的一节内容的，wiki上也有详细的讲述。限于篇幅，这里指讲解一个大概的思路，更详细的介绍请参见wiki或算法导论。RB-tree删除操作的基本思路是这样的，首先按照一般的二叉搜索树进行节点的删除，然后对RB-tree相关节点进行变色或旋转。一般的二叉搜索树删除节点的基本思路是：首先找到待删除节点位置，设为D。如果D同时有左右子树，那么用D的后继（右孩子的最左子节点，该后继最多有一个子节点——右孩子）替代D（注意：这里的替代是只key的替代，color不变，仍为D的color），从而将删除位置转移到该后继节点（成为新的D，为叶子节点或只有右孩子）。于是，我们只需要讨论删除只有一个儿子的节点的情况(如果它两个儿子都为空，即均为叶子，我们任意将其中一个看作它的儿子)，设这个儿子节点为N，这仍然需要分三种情况： 1）D为红 这种情况比较简单。由于D为红色，所以它的父亲和儿子一定是黑色的，我们可以简单的用它的黑色儿子替换它，并不会破坏性质3和性质4。通过被删除节点的所有路径只是少了一个红色节点，这样可以继续保证性质5。 2）D为黑且N为红 如果只是去除这个黑色节点，用它的红色儿子顶替上来的话，会破坏性质5，可能会破坏性质4，但是如果我们重绘它的儿子为黑色，则曾经通过它的所有路径将通过它的黑色儿子，这样可以继续保持性质5，同时也满足性质4。 3）D为黑且N为黑 这是一种复杂的情况。我们首先把要删除的节点D替换为它的（右）儿子N，在新树中（D被N覆盖），设N的父节点为P，兄弟为S，SL为S的左儿子，SR为S的右儿子。此时，以N为根节点的子树的黑高度减少了一，与S为根节点的子树的黑高度不一致，破坏了性质5。为了恢复，可以分为如下情形： 3.1）N为根节点 已经满足所有性质，不需要调整。 3.2） N是它父亲P的左儿子 case1、S为红色：将P改为红色，S改为黑色，以P为中心左旋，旋转后SL为新的S，SL和SR是新的S的左右孩子，此时case1就转化为了case2或case3或case4；注：case2~4中S均为黑色（否则是case1）。 case2、SL、SR同为黑色：将S改为红色，这样黑高度失衡的节点变为P，转到3.1）重新开始判断和调整； case3、SR为黑：此时SL为红（否则是case2）。将S改为红色，SL改为黑色，然后以S为中心右旋，旋转后SL为新的S，而原S成为SR且为红色，这就将case3变成了case4； case4、SR为红：以P为中心左旋，然后交换P和S的颜色，最后将SR改为黑色，即可完成调整。可以看到调整过程与SL的颜色无关。 3.3）N是它父亲P的右儿子 与3.2）类似，这里就不详细展开了。

6. RB-tree的查询操作

RB-tree是一个二叉搜索树，元素的查询是其拿手项目，非常简单，以下是RB-tree提供的查询操作：

template <class _Key, class _Value, class _KeyOfValue, class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::find(const _Key& __k) {
  _Link_type __y = _M_header;      // Last node which is not less than __k. 
  _Link_type __x = _M_root();      // Current node. 

  while (__x != 0) // x为NIL时推出循环
    if (!_M_key_compare(_S_key(__x), __k))
      __y = __x, __x = _S_left(__x); // 往左子树找（赋值运算优先于逗号运算，y是x的父节点）
    else
      __x = _S_right(__x); // 往右子树找

  iterator __j = iterator(__y);
  return (__j == end() || _M_key_compare(__k, _S_key(__j._M_node))) ?
     end() : __j; // 没找到返回end()，否则返回相应节点的指针（迭代器）
}

小结

关于RB-tree基本就介绍到这里了，主要是RB-tree的定义、数据结构、插入删除和查找等基本操作，其中最主要也最困难的就是插入和删除操作中恢复平衡的方法。另外，还介绍了二叉搜索树的基本概念和高度平衡的AVL树，可以看到，AVL树保持平衡的方法非常简单易懂，而RB-tree由于引入了节点的颜色属性，使得理解起来相对比较困难，那么问题就来了，为什么不用AVL-tree而用RB-tree作为set和map的低层容器呢？

这个问题要问STL的实现者了，其实AVL-tree和RB-tree的平均性能在 AVL-tree的wiki _上是有严格的数学公式的，AVL的平均高度为 1.44logN1.44logN ，而RB-tree的平均高度为 2logN2logN ，这些数据的来历也有相关的论文，感兴趣的可以更深入的看看。

关联式容器之set和multiset

本文涉及到 SGI STL 源码的文件主要有 stl_set.h、 stl_multiset.h、 set.h、 multiset.h、 set 等文件。

1. set 简介

set 即集合，相比于其他容器有些特别。首先是它的每个元素是唯一的，即不允许有相同的值出现。其次，作为一种关联容器，set 的元素不像 map 那样可以同时拥有实值（value）和键值（key），set 元素的键值就是实值，实值就是键值。由于 set 的实质和键值相同，共用同一个内存空间，而 set 的底层容器为红黑树（中序遍历有序），因此不能对其键值进行修改，否则会破坏其有序特性。为避免非法修改操作，在SGI STL的实现中，set<T>::iterator 被定义为 RB-tree 底层的 const_iterator，_杜绝写入操作。set 与 list 有一个相似的地方是，元素插入、删除后，之前的迭代器依然有效（被删除的那个元素的迭代器除外）。我们知道集合有一些特殊的操作，诸如并、交、差等，在STL的 set 中，默认也提供了这些操作，如交集 set_intersection 、联集 set_union 、差集 set_difference 和对称差集 set_symmetric_difference 等。与之前那些线性容器不同的是，这些 set 的操作并不是在 set 内部实现的，而是放在了算法模块（algorithm）中，其具体实现在后面的算法章节中会具体介绍。

2. set 的实现

前面多次提到 set 的底层采用 RB-tree 容器，这是因为 RB-tree 是一种比较高效的平衡二叉搜索树，能够很好的满足元素值唯一的条件，而且查找效率高。由于 RB-tree 已实现了很多操作，因此 set 基本上只是对 RB-tree 进行了一层简单的封装。下面是其实现的主要代码：

template <class _Key, class _Compare, class _Alloc>
class set {
public:
  typedef _Key     key_type;
  typedef _Key     value_type; // 实值与键值同类型
private:
  typedef _Rb_tree<key_type, value_type, _Identity<value_type>, key_compare, _Alloc> _Rep_type;
  _Rep_type _M_t;  // 底层使用红黑树作为容器
  set() : _M_t(_Compare(), allocator_type()) {} // 默认构造函数
  set(const set<_Key,_Compare,_Alloc>& __x) : _M_t(__x._M_t) {}  // 拷贝构造函数
  pair<iterator,bool> insert(const value_type& __x) { // 插入操作
    pair<typename _Rep_type::iterator, bool> __p = _M_t.insert_unique(__x);
    return pair<iterator, bool>(__p.first, __p.second);
  }
  void erase(iterator __position) { // 删除操作
    typedef typename _Rep_type::iterator _Rep_iterator;
    _M_t.erase((_Rep_iterator&)__position);
  }
  void clear() { _M_t.clear(); } // 清空操作
  iterator find(const key_type& __x) const { return _M_t.find(__x); } // 查找
  size_type count(const key_type& __x) const { // 计数
    return _M_t.find(__x) == _M_t.end() ? 0 : 1;
  }
};
template <class _Key, class _Compare, class _Alloc>
inline bool operator==(const set<_Key,_Compare,_Alloc>& __x,
                       const set<_Key,_Compare,_Alloc>& __y) { // 比较相等操作符
  return __x._M_t == __y._M_t;
}
template <class _Key, class _Compare, class _Alloc>
inline bool operator<(const set<_Key,_Compare,_Alloc>& __x,
                      const set<_Key,_Compare,_Alloc>& __y) { // 比较大小操作符
  return __x._M_t < __y._M_t;
}

可以看到基本都是调用 _M_t 的方法来实现的，而这里的 _M_t 是一个红黑树对象。

3. multiset

multiset 的特性和用法与 set 基本相同，唯一差别在于它允许有重复的键值，因此它的插入操作使用的底层机制是 RB-tree 的 insert_equal() 而不是 insert_unique() ，下面是 multiset 的主要代码，主要列出了与 set 不同的部分。

template <class _Key, class _Compare, class _Alloc>
class multiset {
public:
  multiset(const value_type* __first, const value_type* __last)
    : _M_t(_Compare(), allocator_type())
    { _M_t.insert_equal(__first, __last); } // 构造函数
  iterator insert(const value_type& __x) { // 插入操作
    return _M_t.insert_equal(__x);
  }
  iterator insert(iterator __position, const value_type& __x) {
    typedef typename _Rep_type::iterator _Rep_iterator;
    return _M_t.insert_equal((_Rep_iterator&)__position, __x);
  }
  void insert(const value_type* __first, const value_type* __last) {
    _M_t.insert_equal(__first, __last);
  }
  void insert(const_iterator __first, const_iterator __last) {
    _M_t.insert_equal(__first, __last);
  }
};

其他部分基本与 set 一样。

关联式容器之map和multimap

本文涉及到 SGI STL 源码的文件主要是 stl_map.h、stl_multimap.h、stl_pair.h、map.h、 multimap.h、 map 等文件。

1. map 简介

map 的特性是，所有元素都是键值对，用一个 pair 表示，pair 的第一个元素是键值（key），第二个元素是实值（value），map 不允许两个元素的键值相同。与 set 类似的，map 也不允许修改 key 的值，但不同的是可以修改 value 的值，因此 map 的迭代器既不是一种 constant iterators，也不是一种 mutable iterators。同样的，map的插入和删除操作不影响操作之前定义的迭代器的使用（被删除的那个元素除外）。与 set 不同的是，map 没有交、并、差等运算，只有插入、删除、查找、比较等基本操作。

2. map 的实现

由于 map 的元素是键值对，用 pair 表示，下面是它的定义：

template <class _T1, class _T2>
struct pair {
  typedef _T1 first_type;
  typedef _T2 second_type;
  _T1 first; // 两个成员 first 和 second
  _T2 second;
  pair() : first(_T1()), second(_T2()) {} // 构造函数
  pair(const _T1& __a, const _T2& __b) : first(__a), second(__b) {} // 拷贝构造函数
};
template <class _T1, class _T2>
inline bool operator==(const pair<_T1, _T2>& __x, const pair<_T1, _T2>& __y) { // 相等比较
  return __x.first == __y.first && __x.second == __y.second;
}
template <class _T1, class _T2>
inline bool operator<(const pair<_T1, _T2>& __x, const pair<_T1, _T2>& __y) { // 大小比较
  return __x.first < __y.first || (!(__y.first < __x.first) && __x.second < __y.second);
}
template <class _T1, class _T2>
inline pair<_T1, _T2> make_pair(const _T1& __x, const _T2& __y) { // 创建一个 pair
  return pair<_T1, _T2>(__x, __y);
}

然后是 map 的定义，大体上和 set 差不多，只是在使用 RB-tree 作为容器时，传入的模板参数是一个 pair，主要代码如下：

template <class _Key, class _Tp, class _Compare, class _Alloc>
class map {
public:
  typedef _Key                  key_type;
  typedef _Tp                   data_type;
  typedef _Tp                   mapped_type;
  typedef pair<const _Key, _Tp> value_type;
  typedef _Compare              key_compare;
  // 一个用于键值比较的内部类
  class value_compare : public binary_function<value_type, value_type, bool> {
  friend class map<_Key,_Tp,_Compare,_Alloc>;
  protected :
    _Compare comp;
    value_compare(_Compare __c) : comp(__c) {}
  public:
    bool operator()(const value_type& __x, const value_type& __y) const {
      return comp(__x.first, __y.first);
    }
  };
private:
  typedef _Rb_tree<key_type, value_type, _Select1st<value_type>,
    key_compare, _Alloc> _Rep_type; // 这里的value_type是一个pair<const _Key, _Tp>
  _Rep_type _M_t;  // 用红黑树作为底层容器
public:
  map() : _M_t(_Compare(), allocator_type()) {} // 默认构造函数
  bool empty() const { return _M_t.empty(); } // 判断是否为空
  size_type size() const { return _M_t.size(); } // 获取元素个数
  map(const value_type* __first, const value_type* __last)
    : _M_t(_Compare(), allocator_type())
    { _M_t.insert_unique(__first, __last); } // 构造函数，使用insert_unique，键值不允许重复
  void insert(const value_type* __first, const value_type* __last) { // 插入操作
    _M_t.insert_unique(__first, __last);
  }
  void erase(iterator __position) { _M_t.erase(__position); } // 删除操作
  iterator find(const key_type& __x) { return _M_t.find(__x); } // 查找操作
};

可以看到，基本也是对底层容器 RB-tree 的一个简单的封装。

3. multimap

multimap 与 map 的关系和 multiset 与 set 的关系一样，即 multimap 允许键值（key）重复，插入操作使用 RB-tree 的 insert_equal ，其他都和 map 一样，这里就不贴源代码了。

关联式容器之hashtable

本文涉及到 SGI STL 源码的文件主要是 stl_hashtable.h、stl_hash_fun.h 等文件。

1. hashtable 简介

在数据结构中我们知道，有种数据结构的插入、删除、查找等操作的性能是常数时间，但需要比元素个数更多的空间，这种数据结构就是哈希表。哈希表的基本思想是，将数据存储在与其数值大小相关的地方，比如对该数取模，然后存储在以余数为下表的数组中。但这样会出现一个问题，就是可能会有多个数据被映射到同一个存储位置，即出现了所谓的“碰撞”。哈希表的主要内容就是解决“碰撞”问题，一般而言有以下几种方法：线性探测、二次探测、开链等。

线性探测

简单而言，就是在出现“碰撞”后，寻找当前位置以后的空档，然后存入。如果找到尾部都没有空档，则从头部重新开始找。只要空间大小比元素个数大，总能找到的。相应的，元素的查找和删除也与普通的数组不同，查找如果直接定位到相应位置并找到或是空档，就可以确定存在或不存在，而如果定位到当前位置非空且与待查找的元素不同，则要依序寻找后续位置的元素，直到找到或移到了空档。删除则是采用懒惰删除策略，即只标记删除记号，实际删除操作则待表格重新整理时再进行。

二次探测

与线性探测类似，但向后寻找的策略是探测距当前位置为平方数的位置，即 $index = H+i^{2}$ 。但这样会有一个问题，那就是能否保证每次探测的是不同的位置，即是否存在某次插入时，探测完一圈后回到自己而出现死循环。

开链

这种方法是将出现冲突的元素放在一个链表中，而哈希表中只存储这些链表的首地址。SGI STL中就是使用这种方法来解决“碰撞”的。

2. hashtable 的数据结构

由于使用开链的方法解决冲突，所以要维护两种数据结构，一个是 hash table，在 STL 中称为 buckets，用 vector 作为容器；另一个是链表，这里没有使用 list 或 slist 这些现成的数据结构，而是使用自定义 __hashtable_node ，相关定义具体如下：

template <class _Val>
struct _Hashtable_node { // 链表节点的定义
  _Hashtable_node* _M_next; // 指向下一个节点
  _Val _M_val;
};
template <class _Val, class _Key, class _HashFcn, class _ExtractKey, class _EqualKey, class _Alloc>
class hashtable {
private:
  typedef _HashFcn hasher;
  hasher                _M_hash; // 哈希函数
  typedef _Hashtable_node<_Val> _Node; // 节点类型别名定义
  vector<_Node*,_Alloc> _M_buckets; // hash table，存储链表的索引
};

这里 hashtable 的模板参数很多，其含义如下：

Val: 节点的实值类型 Key: 节点的键值类型 HashFcn: 哈希函数的类型 ExtractKey: 从节点中取出键值的方法（函数或仿函数） EqualKey: 判断键值相同与否的方法（函数或仿函数） Alloc: 空间配置器，默认使用 std::alloc

虽然开链法并不要求哈希表的大小为质数，但 SGI STL 仍然以质数来设计表的大小，并将28个质数（大约2倍依次递增）计算好，并提供函数来查询其中最接近某数并大于某数的质数，如下：

enum { __stl_num_primes = 28 };
static const unsigned long __stl_prime_list[__stl_num_primes] = {
  53ul,         97ul,         193ul,       389ul,       769ul,
  1543ul,       3079ul,       6151ul,      12289ul,     24593ul,
  49157ul,      98317ul,      196613ul,    393241ul,    786433ul,
  1572869ul,    3145739ul,    6291469ul,   12582917ul,  25165843ul,
  50331653ul,   100663319ul,  201326611ul, 402653189ul, 805306457ul,
  1610612741ul, 3221225473ul, 4294967291ul
}; // 使用无符号长整型（32bit）
inline unsigned long __stl_next_prime(unsigned long __n) {
  const unsigned long* __first = __stl_prime_list;
  const unsigned long* __last = __stl_prime_list + (int)__stl_num_primes;
  const unsigned long* pos = lower_bound(__first, __last, __n); // lower_bound 是泛型算法，后续会介绍
  return pos == __last ? *(__last - 1) : *pos;
}

3. hashtable 的空间配置

节点空间配置

首先只考虑比较简单的情况，即哈希表的大小不需要调整，此时空间配置主要是链表节点的配置，而 hashtable 使用 vector 作为容器，链表节点的空间配置（分配和释放）如下：

typedef simple_alloc<_Node, _Alloc> _M_node_allocator_type;
_Node* _M_get_node() { return _M_node_allocator_type::allocate(1); } // 分配一个节点的空间
void _M_put_node(_Node* __p) { _M_node_allocator_type::deallocate(__p, 1); } // 释放一个节点的空间
_Node* _M_new_node(const value_type& __obj) {
  _Node* __n = _M_get_node();
  __n->_M_next = 0;
  __STL_TRY {
      construct(&__n->_M_val, __obj);
      return __n;
  }
  __STL_UNWIND(_M_put_node(__n));
}
void _M_delete_node(_Node* __n) {
  destroy(&__n->_M_val);
  _M_put_node(__n);
}

插入操作表格重新整理

哈希表的插入操作有两个问题要考虑，一个是是否允许插入相同键值的元素，另一个是是否需要扩充表的大小。在 STL 中，首先是判断新插入一个元素后是否需要扩充，判断的条件是插入后元素的个数大于当前哈希表的大小；而是否允许元素重复则通过提供 insert_unique 和 insert_equal 来解决。相关代码如下：

pair<iterator, bool> insert_unique(const value_type& __obj) {
  resize(_M_num_elements + 1); // 先进行扩充（如有必要）
  return insert_unique_noresize(__obj); // 然后插入
}
iterator insert_equal(const value_type& __obj) {
  resize(_M_num_elements + 1);
  return insert_equal_noresize(__obj);
}
void hashtable<_Val,_Key,_HF,_Ex,_Eq,_All>::resize(size_type __num_elements_hint) { // 扩充表格
  const size_type __old_n = _M_buckets.size();
  if (__num_elements_hint > __old_n) { // 判断是否需要扩充
    const size_type __n = _M_next_size(__num_elements_hint); // 下一个质数
    if (__n > __old_n) {
      vector<_Node*, _All> __tmp(__n, (_Node*)(0), _M_buckets.get_allocator()); // 新的buckets
      __STL_TRY {
        for (size_type __bucket = 0; __bucket < __old_n; ++__bucket) { // 遍历旧的buckets
          _Node* __first = _M_buckets[__bucket];
          while (__first) { // 处理每一个链表
            size_type __new_bucket = _M_bkt_num(__first->_M_val, __n); // 确定当前节点落在新buckets中的位置
            _M_buckets[__bucket] = __first->_M_next; // 指向下一个节点
            __first->_M_next = __tmp[__new_bucket]; // 在新buckets的新索引位置头部插入
            __tmp[__new_bucket] = __first;
            __first = _M_buckets[__bucket]; // 指向旧链表下一个节点
          }
        }
        _M_buckets.swap(__tmp); // 交换新旧buckets，退出后临时buckets __tmp 自动释放
      }
    }
  }
}
template <class _Val, class _Key, class _HF, class _Ex, class _Eq, class _All>
pair<typename hashtable<_Val,_Key,_HF,_Ex,_Eq,_All>::iterator, bool>
hashtable<_Val,_Key,_HF,_Ex,_Eq,_All>::insert_unique_noresize(const value_type& __obj) { // 不允许键值重复
  const size_type __n = _M_bkt_num(__obj);
  _Node* __first = _M_buckets[__n];
  for (_Node* __cur = __first; __cur; __cur = __cur->_M_next)
    if (_M_equals(_M_get_key(__cur->_M_val), _M_get_key(__obj))) // 判断是否存在重复的key
      return pair<iterator, bool>(iterator(__cur, this), false);
  _Node* __tmp = _M_new_node(__obj);
  __tmp->_M_next = __first;
  _M_buckets[__n] = __tmp;
  ++_M_num_elements;
  return pair<iterator, bool>(iterator(__tmp, this), true);
}

允许键值重复的插入操作类似的，只是为了确保相同键值的挨在一起，先要找到相同键值的位置，然后插入。

整体复制和清空

复制和清空时分别涉及空间的分配和释放，所以在这里也介绍一下。首先是复制操作，需要先将目标 hashtable 清空，然后将源 hashtable 的 buckets 中的每个链表一一复制，如下：

template <class _Val, class _Key, class _HF, class _Ex, class _Eq, class _All>
void hashtable<_Val,_Key,_HF,_Ex,_Eq,_All>::_M_copy_from(const hashtable& __ht) {
  _M_buckets.clear(); // 先清空目标 hashtable
  _M_buckets.reserve(__ht._M_buckets.size()); // 大小重置为源 hashtable 的大小
  _M_buckets.insert(_M_buckets.end(), __ht._M_buckets.size(), (_Node*) 0); // 将目标 hashtable 的 buckets 置空
  __STL_TRY {
    for (size_type __i = 0; __i < __ht._M_buckets.size(); ++__i) { // 遍历 buckets
      const _Node* __cur = __ht._M_buckets[__i];
      if (__cur) {
        _Node* __copy = _M_new_node(__cur->_M_val);
        _M_buckets[__i] = __copy;
        for (_Node* __next = __cur->_M_next; __next; __cur = __next,
              __next = __cur->_M_next) { // 复制每个节点
          __copy->_M_next = _M_new_node(__next->_M_val);
          __copy = __copy->_M_next;
        }
      }
    }
    _M_num_elements = __ht._M_num_elements;
  }
  __STL_UNWIND(clear());
}

4. hashtable 的迭代器

hashtable 的迭代器是前向的单向迭代器，遍历的方式是先遍历完一个 list 然后切换到下一个 bucket 指向的 list 进行遍历。以下是 hashtable 的迭代器的定义：

template <class _Val, class _Key, class _HashFcn, class _ExtractKey, class _EqualKey, class _Alloc>
struct _Hashtable_iterator {
  typedef hashtable<_Val,_Key,_HashFcn,_ExtractKey,_EqualKey,_Alloc> _Hashtable;
  typedef _Hashtable_iterator<_Val, _Key, _HashFcn, _ExtractKey, _EqualKey, _Alloc> iterator;
  typedef _Hashtable_const_iterator<_Val, _Key, _HashFcn, _ExtractKey, _EqualKey, _Alloc> const_iterator;
  typedef _Hashtable_node<_Val> _Node;

  _Node* _M_cur; // 指向当前节点
  _Hashtable* _M_ht; // 指向当前节点所在 bucket

  _Hashtable_iterator(_Node* __n, _Hashtable* __tab) : _M_cur(__n), _M_ht(__tab) {}
  _Hashtable_iterator() {}
  reference operator*() const { return _M_cur->_M_val; }
  iterator& operator++();
  iterator operator++(int);
  bool operator==(const iterator& __it) const { return _M_cur == __it._M_cur; }
  bool operator!=(const iterator& __it) const { return _M_cur != __it._M_cur; }
};
template <class _Val, class _Key, class _HF, class _ExK, class _EqK, class _All>
_Hashtable_iterator<_Val,_Key,_HF,_ExK,_EqK,_All>&
_Hashtable_iterator<_Val,_Key,_HF,_ExK,_EqK,_All>::operator++(){
  const _Node* __old = _M_cur;
  _M_cur = _M_cur->_M_next;
  if (!_M_cur) { // 到了当前 bucket 的尾部
    size_type __bucket = _M_ht->_M_bkt_num(__old->_M_val);
    while (!_M_cur && ++__bucket < _M_ht->_M_buckets.size())
      _M_cur = _M_ht->_M_buckets[__bucket];
  }
  return *this;
}

5. 哈希函数

在第三节中介绍 hashtable 的数据结构时，提到了一个哈希函数类型的模板参数，从键值到索引位置的映射由这个哈希函数来完成，实际中是通过函数 _M_bkt_num_key 来完成这个映射的，如下：

size_type _M_bkt_num_key(const key_type& __key) const {
  return _M_bkt_num_key(__key, _M_buckets.size());
}
size_type _M_bkt_num_key(const key_type& __key, size_t __n) const {
  return _M_hash(__key) % __n; // 在这里调用函数 _M_hash，实现映射
}

这里的 _M_hash 是一个哈希函数类型的成员，可以看做是一个函数指针，真正的函数的定义在 <stl_hash_fun.h> 中，针对 char，int，long 等整数型别，这里大部分的 hash function 什么也没做，只是重视返回原始值，但对字符串（const char* ）设计了一个转换函数，如下：

template <class _Key> struct hash { }; // 仿函数 hash
inline size_t __stl_hash_string(const char* __s) { // 将字符串映射为整型
  unsigned long __h = 0;
  for ( ; *__s; ++__s)
    __h = 5*__h + *__s;
  return size_t(__h);
}
__STL_TEMPLATE_NULL struct hash<char*> {
  size_t operator()(const char* __s) const { return __stl_hash_string(__s); } // 函数调用操作符 operator()
};
__STL_TEMPLATE_NULL struct hash<const char*> {
  size_t operator()(const char* __s) const { return __stl_hash_string(__s); }
};
__STL_TEMPLATE_NULL struct hash<char> {
  size_t operator()(char __x) const { return __x; }
};
__STL_TEMPLATE_NULL struct hash<unsigned char> {
  size_t operator()(unsigned char __x) const { return __x; }
};
__STL_TEMPLATE_NULL struct hash<signed char> {
  size_t operator()(unsigned char __x) const { return __x; }
};
__STL_TEMPLATE_NULL struct hash<short> {
  size_t operator()(short __x) const { return __x; }
};
__STL_TEMPLATE_NULL struct hash<unsigned short> {
  size_t operator()(unsigned short __x) const { return __x; }
};
__STL_TEMPLATE_NULL struct hash<int> {
  size_t operator()(int __x) const { return __x; }
};
__STL_TEMPLATE_NULL struct hash<unsigned int> {
  size_t operator()(unsigned int __x) const { return __x; }
};
__STL_TEMPLATE_NULL struct hash<long> {
  size_t operator()(long __x) const { return __x; }
};
__STL_TEMPLATE_NULL struct hash<unsigned long> {
  size_t operator()(unsigned long __x) const { return __x; }
};

关联式容器之hashset和hashmap

本文涉及到 SGI STL 源码的文件主要是 stl_hash_set.h、stl_hash_map.h 等文件。

1. hashset 和 hash_multi_set

需要说明的是，STL 标准只规范了复杂度与接口，并没有规范实现方法，但 STL 实现的版本中 set 大多以 RB-tree 为底层机制，SGI STL 在实现了以 RB-tree 为底层机制的 set 外，还实现了以 hashtable 为底层机制的 hashset。

和 set 一样，hashset 的键值（key）和实值（value）是同一个字段，不同的是 set 默认是自动排序的，而 hashset 则是无序的。除此之外，hashset 与 set 的对外接口完全相同。这里还有一种称为 hash_multi_set 的集合，它同 multiset 类似，允许键值重复，而上面的 hashset 则不允许。下面是 hashset 的定义的主要代码：

template <class _Value, class _HashFcn, class _EqualKey, class _Alloc>
class hash_set {
private:
  typedef hashtable<_Value, _Value, _HashFcn, _Identity<_Value>, _EqualKey, _Alloc> _Ht;
  _Ht _M_ht; // 底层容器的定义
public:
  hash_set() : _M_ht(100, hasher(), key_equal(), allocator_type()) {} // 构造函数
  iterator find(const key_type& __key) const { return _M_ht.find(__key); } // 查找
  size_type count(const key_type& __key) const { return _M_ht.count(__key); } // 计数
  size_type size() const { return _M_ht.size(); } // 表格大小
  size_type max_size() const { return _M_ht.max_size(); }
  bool empty() const { return _M_ht.empty(); } // 是否为空
  void swap(hash_set& __hs) { _M_ht.swap(__hs._M_ht); } // 交换
  iterator begin() const { return _M_ht.begin(); }
  iterator end() const { return _M_ht.end(); }
  pair<iterator, bool> insert(const value_type& __obj){ // 插入
      pair<typename _Ht::iterator, bool> __p = _M_ht.insert_unique(__obj);
      return pair<iterator,bool>(__p.first, __p.second);
  }
  size_type erase(const key_type& __key) {return _M_ht.erase(__key); } // 擦除
  void erase(iterator __it) { _M_ht.erase(__it); }
  void erase(iterator __f, iterator __l) { _M_ht.erase(__f, __l); }
  void clear() { _M_ht.clear(); } // 清空
};
template <class _Value, class _HashFcn, class _EqualKey, class _Alloc>
inline bool operator==(const hash_set<_Value,_HashFcn,_EqualKey,_Alloc>& __hs1,
           const hash_set<_Value,_HashFcn,_EqualKey,_Alloc>& __hs2) {
  return __hs1._M_ht == __hs2._M_ht;
}

2. hashmap 和 hash_multi_map

hashmap 是以 hashtable 为底层容器的 map，而 map 是同时拥有实值（value）和键值（key），且不允许键值重复。

而 hash_multi_map 是以 hashtable 为底层容器的 map，且允许键值重复。

STL 算法

算法

1. 算法概述

算法（Algorithm）是一个计算的具体步骤，常用于计算、数据处理和自动推理。Donald Knuth 在他的著作 The Art of Computer Programming 里对算法的特征归纳（来自wiki）：

输入：一个算法必须有零个或以上输入量。
输出：一个算法应有一个或以上输出量，输出量是算法计算的结果。
明确性：算法的描述必须无歧义，以保证算法的实际执行结果是精确地符合要求或期望，通常要求实际运行结果是确定的。
有限性：依据图灵的定义，一个算法是能够被任何图灵完备系统模拟的一串运算，而图灵机只有有限个状态、有限个输入符号和有限个转移函数（指令）。而一些定义更规定算法必须在有限个步骤内完成任务。
有效性：又称可行性。能够实现，算法中描述的操作都是可以通过已经实现的基本运算执行有限次来实现。

算法的核心是创建问题抽象的模型和明确求解目标，常见的算法有分治法、贪婪算法、动态规划、平摊分析等。再好的编程技巧，也无法让一个笨拙的算法起死回生，选择了错误的算法，便注定了失败的命运。

算法的时间复杂度是指算法需要消耗的时间资源。一般来说，计算机算法是问题规模 nn 的函数 f(n)f(n) ，算法的时间复杂度也因此记做：

T(n)=O(f(n))T(n)=O(f(n))

算法执行时间的增长率与f(n)f(n)的增长率正相关，称作渐近时间复杂度（Asymptotic Time Complexity），简称时间复杂度。常见的时间复杂度有：常数阶 O(1)O(1) ,对数阶 O(log2n)O(log2n) ,线性阶 O(n)O(n) , 线性对数阶 O(nlog2n)O(nlog2n) ,平方阶 $O(n2 )，立方阶，立方阶O(n3 )，…，k次方阶，…，k次方阶O( nk ),指数阶,指数阶O( 2n )。随着问题规模。随着问题规模n$ 的不断增大，上述时间复杂度不断增大，算法的执行效率越低。

算法的空间复杂度是指算法需要消耗的空间资源。其计算和表示方法与时间复杂度类似，一般都用复杂度的渐近性来表示。同时间复杂度相比，空间复杂度的分析要简单得多。

2. STL 算法概览

很多算法能用来解决特定问题（如排序、查找、复制、比较、组合等），并获得数学上的性能分析与证明，这样的算法非常具有复用性，STL 的算法组件就总结了70+ 个极具复用价值的算法，包括排序（sorting）、查找（searching）、排列组合（permutation）等，以及用于数据移动、复制、删除、比较、组合、运算等算法。

某些特定的算法与特定的数据结构相关，例如二叉查找树和红黑树便是为了解决查找问题而发展出来的特殊数据结构，hashtable 拥有快速查找能力，又例如 max-heap 可以协助完成 heap sort，几乎可以说，特定的数据结构是为了实现某种特定的算法。这类与特定数据结构相关的算法，在前几篇介绍容器的文章中都有提到，而接下来几篇文章所要介绍的算法则是无特殊条件限制的空间中的某一段元素区间的算法，即泛型算法。

2.1 STL 算法的一般形式

所有泛型算法的前两个参数都是一对迭代器（iterators），通常称为 first 和 last，用以标识算法的操作区间，STL 习惯采用前闭后开区间表示法，写成 [first, last) ，当 frist==last 时，表示的是空区间。这个 [first, last) 的必要条件是，必须能够进过 increment （累加）操作的反复运用，从 first 到 last，编译器本身无法强求这一点，如果这个条件不成立，会导致无法预料的结果。

前面讲迭代器时我们知道，STL有5类迭代器，他们是input、output、forward、bidirectional、random_access。_每个 STL 算法的声明，都表现出它所需要的最低程度的迭代器类型，例如 find() 需要一个 inputIterators 是最低要求，但也可以接受更高类型的，如 forwardIterators、bidirectionalIterators、randomAccessIterators，但如果传给它一个outputIterators，则会导致错误。将无效的迭代器传给某个算法，虽然是一种错误，却不能保证在编译时期就被捕捉出来，因为所谓的迭代器型别并不是真实的型别，他们只是 function template 的一种型别参数（type parameters）。

许多 STL 算法都有很多个版本，除了默认的只包含迭代器参数的实现之外，还有一个可以传入仿函数（functor）参数的版本，例如 unique() 缺省情况下使用 equality 操作符来比较两个相邻的元素，但如果这些元素的型别并未提供 equality 操作符，或如果用户希望定义自己的 equality 操作符，便可以传一个仿函数给另一个版本的 unique() ，有些算法干脆将这样的两个版本分为两个不同名的实体，如 find_if()、replace_if() 等。

2.2 质变算法与非质变算法

所谓质变算法（mutating algorithms），是指算法运算过程中，会更改区间[first, last)内（迭代器所指）的元素内容，诸如复制（copy）、互换（swap）、替换（replace）、填充（fill）、删除（remove）、排列组合（permutation）、分割（partition）、随机重排（random shuffling）等，都属于此类。通常质变算法提供两个版本，一个是就地（in-place）进行，另一个是copy（另地进行）版本，将操作对象复制一份副本，然后在副本上进行修改并返回该副本。copy版一般以 _copy 作为函数名后缀，例如 replace_copy() 等。但并不是所有的质变算法都提供copy版，例如 sort 就没有。如果我们一定要使用 copy 版，需要我们自己先 copy 一份副本，然后再将副本传给相应的算法。

所谓非质变算法（nonmutating algorithms），是指算法运算过程中不会更改区间[first, last)内的元素内容，诸如查找（find）、匹配（search）、计数（count）、巡访（for_each）_、比较（equal，mismatch）、寻找极值（max、min）等。

2.3 STL 算法的分类

STL 算法的实现主要在 stl_algobase.h、stl_algo.h、stl_numeric.h 这3个文件中，其中 stl_numeric.h 主要是数值（numeric）算法，包括 adjecent_difference()、accumulate()、inner_product()、partial_sum() 等，相关接口封装在 <numeric> 中。而其他算法如复制、填充、交换、求极值、排列、排序、分割等等算法则在剩下的那两个文件中，相关接口则封装在 <algorithm> 中。C++ 的官方文档将 STL 算法分为以下几类：

Non-modifying sequence operations 非质变操作，查找、计数等
Modifying sequence operations 质变操作，复制、交换、替换、填充、删除、逆转、旋转等
Partitions 分割
Sorting 排序
Binary search (operating on partitioned/sorted ranges) 二分查找
Merge (operating on sorted ranges) 合并
Heap、Min/max、Other 堆算法、极值、其他等

后续文章将分别介绍这些算法的具体实现。

3. 算法的泛化

上文提到过，很多算法是与底层的数据结构相关的，如何将算法独立于其所处理的数据结构之外，使它能够处理任何数据结构，或者在未知的数据结构（也许是 array，也许是vector，也许是list，也许是deque）上正确地实现操作，并不那么简单。其关键在于，需要把操作对象的型别加以抽象化，把操作对象的标示法和区间目标的移动行为抽象化。如此，整个算法也就在一个抽象层面了，这个过程称为算法的泛型化（generalized），简称泛化。

下面以查找算法的泛化过程为例详细介绍算法泛化的奇妙。对于查找算法，我们首先想到的是在一个整型数组中查找指定元素，一个基本的实现如下：

int* find(int* arrayHead, int arraySize, int value){
  for(int i=0; i < arraySize; i++){
      if(arrayHead[i] == value) break;
  }
  return &(arrayHead[i]);
}

该函数在数组中查找指定值的元素，返回找到的第一个符合条件的元素的地址，如果没有找到就返回最后一个元素的下一个位置（称为end）。当没有找到时，这里为什么要返回地址值（end）而不返回null呢？这是为了方便调用后续的泛型算法，但实际上该算法本身还是与容器相关的，而且暴露了很多容器的实现细节（如arraySize等）。为了让该算法适用于所有类型的容器，其操作应该更抽象化，可以让 find 接受两个指针作为参数，标识出一个操作区间，如下：

int* find(int* begin, int* end, int value){
  while(begin != end && *begin != value) ++begin;
  return begin;
}

该函数在区间 [begin, end) 内查找 value，并返回一个指针。这样做之后，已经隐藏了容器内部特性了，但不足的是，要求元素的数据类型为整型，我们可以通过模板参数来解决这个问题：

template<typename T>
T* find(T* begin, T* end, const T& value){
  // 用到了operator !=,*,++
  while(begin != end && *begin != value) ++begin;
  return begin; // 会引发copy行为
}

除了参数模板化之外，值得注意的是其中待查找的对象是以常引用的方式传递，这样对于大对象非常有利。于是，现在的find函数几乎适用于任何容器——只要该容器允许指针，而指针又都支持inequality（判断不相等）操作符、dereference（取值）操作符、（prefix）increment（前置式递增）操作符、copy（复制）行为这四种操作。

但这个版本还不够泛化，因为参数被限制为指针，而那些支持以上四种操作、行为很像指针的某些对象就无法使用 find 了。在STL中有迭代器，它是一种行为类似指针的对象，是一种smart pointers，使用迭代器实现 find 如下：

template<class Iterator, class T>
Iterator find(Iterator begin, Iterator end, const T& value){
  while(begin != end && *begin != value) ++begin;
  return begin;
}

这便是一个完全泛化的find 函数，它与STL中的find函数几乎一模一样（不同之处可自行查看STL源码）。了解和理解了STL算法的泛化过程，就很容易看懂STL中很多其他的算法了。

算法之数值算法

本文主要介绍STL中的数值算法，主要涉及到的源码文件有 stl_numberic.h、numeric、stl_relops.h 等。

STL 数值算法主要包含以下几个算法（来自C++文档）：

accumulate: Accumulate values in range
adjacent_difference: Compute adjacent difference of range
inner_product: Compute cumulative inner product of range
partial_sum: Compute partial sums of range
iota: Store increasing sequence
power: power(x,n) 1 multiply by x n times (not in C++ standard)

下面一一介绍每个算法的实现。

1. accumulate

该算法计算 init 和区间 [first, last) 内所有元素的总和。注意，必须提供 init 的初始值，这样即使 first=last 区间为空，仍能得到一个明确定义的值。当 init=0 时，即为计算 [first, last) 区间内所有元素的总和。具体实现有两个版本，如下：

template <class _InputIterator, class _Tp>
_Tp accumulate(_InputIterator __first, _InputIterator __last, _Tp __init){
  __STL_REQUIRES(_InputIterator, _InputIterator); // concept check
  for ( ; __first != __last; ++__first)
    __init = __init + *__first; // 求和
  return __init;
}
template <class _InputIterator, class _Tp, class _BinaryOperation>
_Tp accumulate(_InputIterator __first, _InputIterator __last, _Tp __init, _BinaryOperation __binary_op){
  __STL_REQUIRES(_InputIterator, _InputIterator); // concept check
  for ( ; __first != __last; ++__first)
    __init = __binary_op(__init, *__first); // 指定二元操作
  return __init;
}

第二个版本通过仿函数参数 binary_op 指定操作类型，可以实现其他方式的累计，例如累乘等（令init=1，binary_op=multiply）。

2. adjacent_difference

该算法用来计算区间 [first, last) 中相邻元素的差（或其他指定运算，结果[i]=当前元素[i]的值-前驱元素[i-1]的值），该算法也有两个版本，一个是指定运算为差，另一个传入仿函数(参数 _binary_op)指定具体运算，这里贴出第二个版本：

template <class _InputIterator, class _OutputIterator, class _Tp, class _BinaryOperation>
_OutputIterator
__adjacent_difference(_InputIterator __first, _InputIterator __last,
                      _OutputIterator __result, _Tp*, _BinaryOperation __binary_op) {
  _Tp __value = *__first;
  while (++__first != __last) { // 先 ++ ，再比较
    _Tp __tmp = *__first; // 取第i+1个元素的值
    *++__result = __binary_op(__tmp, __value);
    __value = __tmp; // 保存第i个元素的值
  }
  return ++__result;
}
template <class _InputIterator, class _OutputIterator, class _BinaryOperation>
_OutputIterator adjacent_difference(_InputIterator __first, _InputIterator __last,
                    _OutputIterator __result, _BinaryOperation __binary_op) {
  if (__first == __last) return __result; // 区间为空，直接返回
  *__result = *__first; // 第一个元素没有前驱，直接将当前值赋给结果
  return __adjacent_difference(__first, __last, __result,
                               __VALUE_TYPE(__first), __binary_op);
}

3. inner_product

该算法实现区间 [first1, last1) 和区间 [first2, first2+(last1-first1) ) 的一般内积（generalized inner product），公式为$init = init+(i) * ((first2+(i-first1)))$同样需要提供 init 的值（理由同accumulate）。另外还有一个版本，提供两个仿函数，分别指定上面公式中的加法和乘法。第一个版本的代码如下：

template <class _InputIterator1, class _InputIterator2, class _Tp>
_Tp inner_product(_InputIterator1 __first1, _InputIterator1 __last1,
                  _InputIterator2 __first2, _Tp __init) {
  for ( ; __first1 != __last1; ++__first1, ++__first2)
    __init = __init + (*__first1 * *__first2);
  return __init;
}

可以看到，这里其实没有判断第二个区间是否越界，所以在调用时需要我们自己注意，但一般来说计算内积的两个区间都是相同长度的。

4. partial_sum

该算法用来计算局部总和，将 *first 赋值给 *result，将 *frist+*(first+1) 赋值给 *(result+1)，依次类推，即有 result[i]=sum(*first..*(first+i))，这是默认的操作为加法的版本，还有一个版本可以通过仿函数指定操作，以下是默认版本：

template <class _InputIterator, class _OutputIterator, class _Tp>
_OutputIterator __partial_sum(_InputIterator __first, _InputIterator __last,
              _OutputIterator __result, _Tp*) {
  _Tp __value = *__first;
  while (++__first != __last) {
    __value = __value + *__first;
    *++__result = __value; // result 先++，再提领、赋值
  }
  return ++__result;
}
template <class _InputIterator, class _OutputIterator>
_OutputIterator partial_sum(_InputIterator __first, _InputIterator __last,
            _OutputIterator __result){
  if (__first == __last) return __result;
  *__result = *__first; // 第一项直接赋值
  return __partial_sum(__first, __last, __result, __VALUE_TYPE(__first));
}

5. itoa

该算法不是C++/STL标准，主要作用是将区间 [first, last) 的值赋值为 value,value+1,value+2,… 如下：

template <class _ForwardIter, class _Tp>
void iota(_ForwardIter __first, _ForwardIter __last, _Tp __value){
  while (__first != __last)
    *__first++ = __value++;
}

6. power

该算法也不是C++/STL标准，作用在于实现 x 的 n 次方的计算，通过将n分解为2的幂来计算。还有一个版本是用户可以指定运算，而不一定是乘法。默认版本如下：

template <class _Tp, class _Integer, class _MonoidOperation>
_Tp __power(_Tp __x, _Integer __n, _MonoidOperation __opr){ // func1：幂方的具体实现
  if (__n == 0)
    return identity_element(__opr);
  else {
    while ((__n & 1) == 0) { // 二进制末尾为0
      __n >>= 1; // n/2
      __x = __opr(__x, __x); // 乘方
    }
    _Tp __result = __x;
    __n >>= 1;
    while (__n != 0) {
      __x = __opr(__x, __x); // 乘方
      if ((__n & 1) != 0) // 二进制末尾为1
        __result = __opr(__result, __x); // 乘入结果
      __n >>= 1;
    }
    return __result;
  }
}
template <class _Tp, class _Integer>
inline _Tp __power(_Tp __x, _Integer __n){ // func2
  return __power(__x, __n, multiplies<_Tp>()); // 调用func3
}
template <class _Tp, class _Integer, class _MonoidOperation>
inline _Tp power(_Tp __x, _Integer __n, _MonoidOperation __opr){ // func3
  return __power(__x, __n, __opr); // 调用func1
}
template <class _Tp, class _Integer>
inline _Tp power(_Tp __x, _Integer __n){
  return __power(__x, __n); // 调用func2
}

饶了几道弯，主要看 func1实现即可。

算法之基本算法algobase

本文主要介绍STL中的基本算法，主要涉及到的源码文件有 stl_algobase.h 等。

在 stl_algobase.h 中定义的算法都比较简单基础，主要涉及区间相等判断、区间填充、求极值、交换、拷贝、字典序比较等算法，而其他诸如查找、计数、排序、旋转等算法则在文件 stl_algo.h 中实现。在algobase基本算法中，除了字典序比较、复制/拷贝算法外，其他都比较简单，这里先依次介绍这些简单的算法，然后再介绍字典序比较和拷贝算法。

1. 交换、填充等简单算法

由于这里很多算法比较简单（基本都在10行以内，甚至很多就一行代码），就不一一粘贴代码了。

iter_swap ：将两个 ForwardIterators 所指的对象对调，通过申请一个临时变量、三次赋值，就完成了。

min/max ：求两个数中的小、大者，还有一个版本可以指定的比较方法（仿函数）。

fill ：将 [first, last) 内的所有元素改填为新值 value。

fill_n ：将 [first, last) 内的前n个元素改填为新值 value，返回迭代器指向被填入的最后一个元素的下一位置。

mismatch ：用来平行比较两个序列，指出两者之间的第一个不匹配点，返回一对迭代器（Iterators Pair），分别指向两序列中的不匹配点。

equal ：判断两个序列在 [first, last) 区间内相等，如果第二个序列元素较多，将不予考虑，只有两个序列在各自区间内对应相等才返回true，否则返回false。

2. 字典序比较

lexicographical_compare 以“字典序排列方式”对两个序列 [first, last) 和 [first2, last2) 进行比较。比较操作针对两个序列中的对应位置上的元素进行，直到某一对不相等或同时到达尾部或仁义序列到达尾部。该算法其实并不复杂，但有一点值得注意，那就当且仅当第一个序列字典序小于第二个序列时才返回true，以下是各种情况下的返回值：

发现不相等，如果第一序列元素较小，返回true，否则返回false；
到达last1而尚未到达last2，返回true；
到达last2而尚未到达last1，返回false；
同时到达last1和last2，返回false。

源码如下：

template <class _InputIter1, class _InputIter2>
bool lexicographical_compare(_InputIter1 __first1, _InputIter1 __last1, _InputIter2 __first2, _InputIter2 __last2) {
  for ( ; __first1 != __last1 && __first2 != __last2; ++__first1, ++__first2) {
    if (*__first1 < *__first2)
      return true;
    if (*__first2 < *__first1)
      return false;
  }
  return __first1 == __last1 && __first2 != __last2;
}

除了这个默认的版本外，还有一个版本提供比较方法（仿函数）的参数。另外，对于纯字符串的比较，SGI STL还做了进一步优化，使用原生指针和C标准函数 memcmp() 进行比较，如下：

inline bool
lexicographical_compare(const unsigned char* __first1, const unsigned char* __last1,
                        const unsigned char* __first2,const unsigned char* __last2) {
  const size_t __len1 = __last1 - __first1;
  const size_t __len2 = __last2 - __first2;
  const int __result = memcmp(__first1, __first2, min(__len1, __len2));
  return __result != 0 ? __result < 0 : __len1 < __len2;
}

3. 复制/拷贝算法

在很多应用程序中，复制copy是一个很常见的操作，特别是在赋值的时候。对于稍微复杂的对象，在不同的语言中赋值时会有一些差别，有的编程语言赋值仅仅是对等号右边的对象的一个引用，而并没有正真的产生一个新的对象，更不用说对象中可能包含的对象成员，例如Python当中的赋值、浅拷贝copy和深拷贝deepcopy等。

而STL 中的copy，除了简单的单一对象的拷贝之外，还有序列区间的拷贝等，这里就涉及到空间分配和时间效率问题。在C++中，复制操作主要是运用assignment operator（复制运算符）或 copy constructor（拷贝构造函数），在STL的copy算法中使用的是前者，而对于某些具有trivial assignment operator的数据，则可以使用内存直接复制行为（例如C标准库函数memmove、memcpy等），就能极大的节省时间。SGI STL用尽各种办法，包括函数重载、型别特性、偏特化（partial specialization）等技巧（关于偏特化请参见 C++模板特化与偏特化），无所不用其极地加强效率。

除了上面提到的元素型别、偏特化等问题，还有元素复制顺序的问题。copy 算法是将原始区间 [first, last) 内的元素复制到目标区间 [result, result+last-first) 区间内，复制时既可以从 first 开始往 last 复制，但也可以从 last-1开始向 first 复制，后者在 STL 另取名为 copy_backward_。从后往前复制的好处在于，不用担心目标区间与原始区间有重叠，因为如果有重叠区域，那么简单的 copy 时，对于原始数据而言 [result, last) 区间的数据在被复制前被修改了，从而得不到预期的结果。当然，有一种情况使用 copy 不用担心这个问题，那就是对于迭代器为原生指针，使用 memmove （而不是 memcpy，关于二者的区别参见 memcpy() vs memmove()）进行复制，此时 memmove 会先将整个区间复制下来，没有被覆盖的危险。

在介绍 copy 算法的源码具体实现前，根据源码及其注释再做一个简单的小结：copy 算法中的一些辅助函数有两个目的，其一是对于简单的数据类型尽量使用 memmove，其二是对于具有 RandomAccessIterators 的对象使用一个计数器来进行循环；除此之外，SGI STL针对编译器是否具有函数模板偏特化、类模板偏特化等进行了适配。下面是 copy 的源码，其中添加了比较详细具体的注释：

// 首先是几个与偏特化无关的公用的3个函数
template <class _InputIter, class _OutputIter, class _Distance>
inline _OutputIter
__copy(_InputIter __first, _InputIter __last,
       _OutputIter __result,input_iterator_tag, _Distance*){
  for ( ; __first != __last; ++__result, ++__first) // 使用迭代器遍历和复制
    *__result = *__first;
  return __result;
}
template <class _RandomAccessIter, class _OutputIter, class _Distance>
inline _OutputIter
__copy(_RandomAccessIter __first, _RandomAccessIter __last,
       _OutputIter __result, random_access_iterator_tag, _Distance*){
  for (_Distance __n = __last - __first; __n > 0; --__n) { //对于随机访问迭代器，使用一个计数器n
    *__result = *__first;
    ++__first;
    ++__result;
  }
  return __result;
}
template <class _Tp>
inline _Tp*
__copy_trivial(const _Tp* __first, const _Tp* __last, _Tp* __result) {
  memmove(__result, __first, sizeof(_Tp) * (__last - __first)); // 直接使用 memmove
  return __result + (__last - __first);
}
//============== __STL_FUNCTION_TMPL_PARTIAL_ORDER 对于具有函数模板偏特性的编译器
#if defined(__STL_FUNCTION_TMPL_PARTIAL_ORDER)
template <class _InputIter, class _OutputIter>
inline _OutputIter
__copy_aux2(_InputIter __first, _InputIter __last, _OutputIter __result, __false_type) { // false_type 的重载版
  return __copy(__first, __last, __result, __ITERATOR_CATEGORY(__first), __DISTANCE_TYPE(__first));
}
template <class _InputIter, class _OutputIter>
inline _OutputIter
__copy_aux2(_InputIter __first, _InputIter __last, _OutputIter __result, __true_type) { // true_type 的重载版
  return __copy(__first, __last, __result, __ITERATOR_CATEGORY(__first), __DISTANCE_TYPE(__first));
}
#ifndef __USLC__
template <class _Tp>
inline _Tp*
__copy_aux2(_Tp* __first, _Tp* __last, _Tp* __result, __true_type) { // 原生指针的重载版
  return __copy_trivial(__first, __last, __result);
}
#endif /* __USLC__ */
template <class _Tp>
inline _Tp*
__copy_aux2(const _Tp* __first, const _Tp* __last, _Tp* __result, __true_type) { // 常量指针的重载版
  return __copy_trivial(__first, __last, __result);
}
template <class _InputIter, class _OutputIter, class _Tp>
inline _OutputIter
__copy_aux(_InputIter __first, _InputIter __last, _OutputIter __result, _Tp*) {
  typedef typename __type_traits<_Tp>::has_trivial_assignment_operator _Trivial;
  return __copy_aux2(__first, __last, __result, _Trivial());
}
template <class _InputIter, class _OutputIter>
inline _OutputIter
copy(_InputIter __first, _InputIter __last, _OutputIter __result) { //最终的对外接口
  return __copy_aux(__first, __last, __result, __VALUE_TYPE(__first));
}
//============== __STL_CLASS_PARTIAL_SPECIALIZATION 对于具有类模板偏特性的编译器
#elif defined(__STL_CLASS_PARTIAL_SPECIALIZATION)
template <class _InputIter, class _OutputIter, class _BoolType>
struct __copy_dispatch { // 类1，泛化版
  static _OutputIter copy(_InputIter __first, _InputIter __last, _OutputIter __result) {
    typedef typename iterator_traits<_InputIter>::iterator_category _Category;
    typedef typename iterator_traits<_InputIter>::difference_type _Distance;
    return __copy(__first, __last, __result, _Category(), (_Distance*) 0);
  }
};
template <class _Tp>
struct __copy_dispatch<_Tp*, _Tp*, __true_type>{ // 类2，特化版
  static _Tp* copy(const _Tp* __first, const _Tp* __last, _Tp* __result) {
    return __copy_trivial(__first, __last, __result);
  }
};
template <class _Tp>
struct __copy_dispatch<const _Tp*, _Tp*, __true_type>{ // 类3，特化版
  static _Tp* copy(const _Tp* __first, const _Tp* __last, _Tp* __result) {
    return __copy_trivial(__first, __last, __result);
  }
};
template <class _InputIter, class _OutputIter>
inline _OutputIter
copy(_InputIter __first, _InputIter __last, _OutputIter __result) { // 对外接口
  typedef typename iterator_traits<_InputIter>::value_type _Tp;
  typedef typename __type_traits<_Tp>::has_trivial_assignment_operator _Trivial;
  return __copy_dispatch<_InputIter, _OutputIter, _Trivial>
    ::copy(__first, __last, __result);
}
//============== 其他，完全不具有偏特化特性的情况
#else /* __STL_CLASS_PARTIAL_SPECIALIZATION */
template <class _InputIter, class _OutputIter>
inline _OutputIter
copy(_InputIter __first, _InputIter __last, _OutputIter __result){ // 对外接口，泛化版
  return __copy(__first, __last, __result, __ITERATOR_CATEGORY(__first), __DISTANCE_TYPE(__first));
}

#define __SGI_STL_DECLARE_COPY_TRIVIAL(_Tp)                                \
  inline _Tp* copy(const _Tp* __first, const _Tp* __last, _Tp* __result) { \ // 对外接口，特化版
    memmove(__result, __first, sizeof(_Tp) * (__last - __first));          \
    return __result + (__last - __first);                                  \
  }

__SGI_STL_DECLARE_COPY_TRIVIAL(char)
__SGI_STL_DECLARE_COPY_TRIVIAL(signed char)
__SGI_STL_DECLARE_COPY_TRIVIAL(unsigned char)
__SGI_STL_DECLARE_COPY_TRIVIAL(short)
__SGI_STL_DECLARE_COPY_TRIVIAL(unsigned short)
__SGI_STL_DECLARE_COPY_TRIVIAL(int)
__SGI_STL_DECLARE_COPY_TRIVIAL(unsigned int)
__SGI_STL_DECLARE_COPY_TRIVIAL(long)
__SGI_STL_DECLARE_COPY_TRIVIAL(unsigned long)
#ifdef __STL_HAS_WCHAR_T
__SGI_STL_DECLARE_COPY_TRIVIAL(wchar_t)
#endif
#ifdef _STL_LONG_LONG
__SGI_STL_DECLARE_COPY_TRIVIAL(long long)
__SGI_STL_DECLARE_COPY_TRIVIAL(unsigned long long)
#endif
__SGI_STL_DECLARE_COPY_TRIVIAL(float)
__SGI_STL_DECLARE_COPY_TRIVIAL(double)
__SGI_STL_DECLARE_COPY_TRIVIAL(long double)
#undef __SGI_STL_DECLARE_COPY_TRIVIAL
#endif /* __STL_CLASS_PARTIAL_SPECIALIZATION */

以上是 copy 的完整代码，关于复制还有两个接口，一个是 copy_n，另一个是 copy_backward，前者复制区间 [first, last) 中前 n 个元素，后者从last-1 往 first 复制，这里就不详细展开了。

算法之复杂算法algorithm

本文主要介绍STL中的稍微复杂的算法，主要涉及到的源码文件有 stl_algo.h 等。

在文件 stl_algo.h 中有很多常用的算法，包括查找、计数、旋转、删除、排序、合并、集合的交并等运算、求极值、排列组合等等，本文将按源码中各算法的实现顺序来介绍其具体实现细节。由于本文涉及到的算法和相关代码太多，在文中就尽量不贴出代码了，详细的代码及相关注释请参见 stl_algo.h。

1. 求三个数的中值 median 该算法比较简单，几个if-else语句就解决了。该函数只提供内部算法使用，并不对外提供接口，也不是STL标准中的算法，限于篇幅这里就不贴代码了。另外，该算法有两个版本，一个是使用默认的大小比较，另一个是可以指定比较函数。

2. for_each 也很简单，就是对区间 [first, last) 中的每一个元素执行一个给定函数的运算，就一行语句：

for ( ; __first != __last; ++__first) __f(*__first);

其中 __f 为用户传入的一个指定的仿函数。该算法的返回值仍为传入的仿函数 __f 。

3. 查找 find 函数 find 查找特定值的元素，函数 find_if 查找经过用户的指定函数 func（STL中的pred函数）运算后结果为 true 的元素。主要代码也只有一行：

while (__first != __last && !(*__first == __val)) ++__first;

另外，关于find，考虑偏特化特性，还有在迭代器为随机存取迭代器时，每次循环进行4次判断和自增，这是所谓的 loop unrolling，在StackOverflow 上也有相关解释 questions-24295972。如果学过体系结构，应该也会提及循环展开的加速方法。

还有一个称为 adjacent_find 的查找算法，它查找序列区间中连续相等的两个元素的位置，返回其中第一个元素的迭代器。这个算法就没有做过多的优化和加速考虑了。

初次之外，在algo文件的最后部分，还有 find_first_of、find_end、`` 的算法，后面会按顺序介绍到。

4. 计数 count 该算法查找序列中值与给定值相等的元素的个数，即进行计数，返回为void，计数结果通过传入的引用参数 _Size& __n 来返回给用户，主要代码如下：

for ( ; __first != __last; ++__first)
    if (*__first == __value) ++__n;

以上这个是非STL标准的，另外还有一个版本返回值为迭代器的 difference_type 的偏特化版本，这个才是STL标准。

5. 搜索search 该算法实现的功能是在区间 [first1, last1) 中搜索是否存在与区间 [first2, last2) 中元素都对应相等的子序列，存在则返回区间1中与区间2匹配的起始位置，否则返回last1。基本思路也很简单，详见源码中我的注释。还有一个版本，可以指定判断条件，而不一定是对应相等这个条件。

另外，还有一个 search_n 的算法与之相似，只是这个算法搜索区间中是否存在长度为count且值均为val的子序列，存在则返回该子序列的起始位置，否则返回last。同样，它也有一个可以指定判断条件的重载版本。

6. 区间置换 swap_ranges 交换两个长度相等的区间：

for ( ; __first1 != __last1; ++__first1, ++__first2)
    iter_swap(__first1, __first2); // 迭代器的交换，使用iter_swap

7. 区间变换运算 transform 对区间的每个元素进行opr运算，结果放在result中，仅这一点与 for_each 不同：

for ( ; __first != __last; ++__first, ++__result)
    *__result = __opr(*__first);

还有一个版本是两个等长序列的运算，结果放在result中：

for ( ; __first1 != __last1; ++__first1, ++__first2, ++__result)
    *__result = __binary_op(*__first1, *__first2);

注意该算法不需要传入第二个区间的last迭代器。

8. 替换 replace 将序列中所有值为oldval的元素值都改为newval：

for ( ; __first != __last; ++__first)
   if (*__first == __old_value) *__first = __new_value;

另外还有三个版本的替换： replace_if，判断条件可以自己指定，而不一定是相等；replace_copy，将修改后的结果存到一个新的序列中；replace_copy_if 是前两者的合体。

9.生成 generate 将序列中的元素的值按给定函数赋值：

for ( ; __first != __last; ++__first) *__first = __gen();

还有一个 generate_n 将序列中的前n个元素的值按给定函数赋值。

10.移除 remove 移除序列中值为val的元素，与 replace 算法类似，有4个版本，其中 remove 和 remove_if 分别通过 remove_copy、remove_copy_if 实现，只需将后者中的result参数设为该序列的起点first。

__first = find(__first, __last, __value);
_ForwardIter __i = __first;
return __first == __last ? __first
                   : remove_copy(++__i, __last, __first, __value);

11.unique和unique_copy 将区间的元素的值唯一化，即去掉相邻的重复的项。由于判断时是针对相邻的元素，所以一般需要结合sort使用，如果序列无序需要先对序列排序再进行唯一化。unique 的实现是调用 unique_copy 来实现的，只是将参数中result仍设为输入序列的first。

这个算法实现的过程中，有很多函数的调用，其中还有个问题没有解决（见代码中注释关于func4什么时候调用func3，func8什么时候调用func7的问题）。

12.反转 reverse 将区间中元素进行反转，一下是迭代器为随机存取迭代器时的实现：

while (__first < __last) iter_swap(__first++, --__last);

还有迭代器为双向迭代器的版本和非质变算法版本 reverse_copy。

13.旋转 rotate 该算法将区间 [first, last) 内的数据以 middle 为分界前后对调，即将[first,middle)+[middle,last) 变为 [middle,last)+[first,middle)。具体实施过程分为两步：首先将middle之后的元素全部调到middle之前，然后对middle之后的元素进行调整，使之按在middle之前时的顺序排列。具体步骤见源码注释，可以结合实例进行理解。该算法的时间复杂度为 O(n)O(n)，总体上只对序列进行了一次遍历。

另外，除了迭代器为前向迭代器的版本之外，还有迭代器为双向迭代器、随机访问迭代器的版本，分别对算法进行了特化和优化，详见源码注释。其中迭代器为随机访问迭代器时，算法稍微复杂些，但可以通过实例来简化理解。关于旋转算法的几种实现及其效率，可以参见这个【Vector Rotation】，其中三种算法分别对应于STL中的随机迭代器版、前向迭代器版、双向迭代器版。虽然三种算法的复杂度均为线性的，但对于大量数据的旋转，还是会存在一些明显的效率区别的。

14.随机相关算法 random random_shuffle 算法将序列随机重排，具体实现是对序列中每个位置的元素与序列中一个随机的元素进行对调：

for (_RandomAccessIter __i = __first + 1; __i != __last; ++__i)
    iter_swap(__i, __first + __random_number((__i - __first) + 1));

除了这个版本采用STL的random函数生成随机数的版本外，还有一个版本可以自己指定随机数生成函数。

random_sample_n 和 random_sample 都是从序列中随机选取n个样本，不同的是输入参数的形式、返回序列的有序性等，均非STL标准。

15.分割 partition 该算法的功能是将序列按条件分割成两个子序列（实际还是一个序列，只是按分割点分成了满足条件的部分和不满足条件的部分），返回分割点的位置。有迭代器为前向迭代器、双向迭代器的版本，保证稳定性的版本 stable_partition。

16. 排序 sort 排序算法是STL中最重要也最复杂的算法，总代码量大概是600行（实际上还不止，因为还有调用其他函数，如partition、merge等），占整个文件的1/5。该算法接受两个随机存取迭代器参数，将区间内的元素以渐增的顺序排列，重载版本则允许用户指定一个仿函数作为排序标准。STL的所有关系型容器都拥有自动排序功能（因为底层是RB-tree，属于有序搜索树），不需要用到这个sort算法，而序列式容器中的stack、queue和priority-queue都有特定的出入限制，不允许排序，剩下vector、deque和list、slist，前两者的迭代器都是随机存取迭代器，可以使用sort算法，而list是双向迭代器，slist是前向迭代器，都不适合使用sort算法，如果要对list或slist排序，需要使用list或slist自己实现的sort函数。

insert_sort 插入排序：在序列长度较小时（STL中设置的是长度小于16时），使用线性（而不是二分）插入排序。

sort 排序：在序列较长时，将序列分割为一个个小的区间，使得区间与区间之间整体上有序，然后使用线性插入排序对整体进行排序。（这与我们通常所理解的快速排序还是有很大区别的，最后整体上进行直接插入排序，实际效果与对每个子区间分别进行插入排序的效果是一样的，效率依然是非常高的）

stable_sort 稳定排序：实际上为归并排序，或称为merge sort，时间复杂度仍为 O(nlogn)O(nlogn)。当子区间长度小于15时，让然是直接用插入排序；当子能够申请到O(n)的buffer时，借助buffer进行merge sort，否则使用inplace merge进行stable sort。而关于两种（with buffer和inplace的）merge的算法的内容，在后文中介绍。

partial_sort 部分排序：使用堆进行排序，功能是将序列 [first, last) 中的较小的 middle-first 个元素排序并放在区间 [first, middle) 中，而其余的 last-middle 个元素仍然是无序的。整个算法分为两个大的步骤，首先是将middle前的元素构建一个max-heap，将middle及之后的元素中比max-heap堆顶小的元素与堆顶对调并调整堆，从而得到middle前的元素都比middle后的元素小；然后使用heap sort对middle之前的元素进行排序。

17. 第n大的数 nth_element 该算法的功能是求一个序列中排行第n大的元素，具体实现时是使用 partition 将搜索范围逐步缩小，直到不足3个元素的区间后，进行insert-sort，最后第n大的元素就位于序列的第n个位置（该算法的迭代器也要求是随机存取的迭代器）。

18. 二分查找 binary_search 该系列算法的前提条件是序列已经有序，迭代器至少是ForwardIterators。

lower_bound ：二分查找 val，存在则返回指向该元素的迭代器，否则返回最小的不小于 val 的元素的迭代器，即在不破坏次序的情况下val可插入的第一个位置。

upper_bound ：二分查找 val，存在则返回该元素的下一个元素的迭代器，否则返回最小的不小于 val的元素的迭代器，及在不破坏次序的前提下，val可插入的最后一个位置。

equal_range ：二分查找 val，返回值为 val 的区间 [i,j)，其中 i 是 lower_bound，而 j 是 upper_bound。

binary_search ：二分查找，找到返回true，否则返回false。实际上使用的是 lower_bound 来实现的。

19. 合并 merge merge ：两个有序序列合并为一个有序序列，输入为5个参数，分别为两个序列的首尾迭代器、结果的首迭代器，算法返回结果序列的尾迭代器。基本思路是同时访问两个序列，取较小者放入结果序列并后移，最后必然是一个序列结束而另一个序列还有剩余元素，只需要将剩余部分copy的结果序列的尾部即可。

inplace_merge：原地将一个序列的两个有序子序列合并，实际上并不一定是原地进行，当可以申请到 O(n)的内存时借助buffer来进行merge，否则进行原地合并。原地合并的基本思路如下：先比较两个有序子序列的长度，将其中较长的序列分成两等分，取该序列的中间元素 first_cut 作为基准，然后得到第二个子序列以该基准分割的位置 second_cut，再然后进行原地旋转，将两个cut之间大于基准的数据旋转到两个cut之间小于基准的数据的后面，这样两个序列就被分成了两对有序子序列，最后分别将小于和大于基准的每对有序子序列进行merge。

20. 集合算法 set 由于集合的低层容器是红黑树，因此集合中的元素是有序的，这样在遍历两个集合时，复杂度不是O(mn)，而是O(m+n)。

includes：判断集合1是否包含集合2. 基本思想是，遍历两个集合，依次判断集合2中的元素是否均在集合1中出现了。

set_union：求两个集合的并集，如果两个集合中出现了相同的元素，则只算一次。

set_intersection：求两个集合的交集，即只保留两个集合中都存在的元素。

set_difference：两个集合的差集，即集合1中存在而集合2中不存在的元素。

set_symmetric_difference：两个集合的对称差，即集合1中存在而2中不存在的元素或集合2中存在而集合1中不存在的元素。

21. 求极值 max/min element 遍历整个区间，找到其中最大/小的元素的值，返回的是指向最大/小值的迭代器。

22. 排列的后继和前驱 next/pre permutation 关于该算法在之前的一篇文章中有详细介绍，请参见全排列及某排列的后继的求解及其STL实现的分析 .

23. 找第一次出现的位置 find first of 在第一个序列中依次查找第二个序列中某个元素第一次出现的位置，使用一个双重循环，外循环遍历第一个序列，内循环遍历第二个序列，只要找到一个就立即返回在序列1中的位置，没有找到则返回序列1的尾迭代器。

24. 查找序列中的子序列 find end 在序列1中查找是否存在序列2这样的子序列，返回最后一次查找结果。还有一个版本是针对双向迭代器的类偏特化版本。

25. 判断序列是否为堆 is heap 判断一个序列是否为堆，即不断地判断父节点是否大于其孩子节点，如果不大于则返回false，否则返回true。

26. 判断序列是否有序 is sorted 判断一个序列是否有序，只需要遍历序列并判断相邻的两个元素的大小关系是否一致即可。

Well Done！终于看完了这些算法了！其中旋转、排序、查找、合并算法是稍微复杂的，且做了一些优化，是需要仔细阅读和体会的。

STL 函数对象

1. 仿函数|函数对象概述

在STL的六大组件中，仿函数可说是体积最小、观念最简单、实现最容易的一个，但小兵也能立大功——他扮演一种“策略”角色，可以让STL算法具有更加灵活的“演出”。

在STL的历史上，仿函数(functor)是早期的命名，C++标准规格定下来后采用了新的名称——函数对象(function object)。就实际意义而言，函数对象的称谓更加贴切：一种具有函数特质的对象。函数对象对调用者而言可以向函数调用一样地被调用，而对被调用者而言则是以对象所定义的函数调用操作符(function call operator)。

在C++中，函数调用操作符是指左右小括弧 () ，该操作符是可以重载的。许多 STL 算法都提供了两个版本，一个用于一般情况（例如排序时使用 operator< 以递增方式排列），一个用于特殊情况（例如排序时按照使用者自定义的大小关系进行排序）。这有点类似于C语言中的函数指针，但函数指针无法满足STL对抽象性的要求，也不能和STL其他组件（如配接器adaptor）搭配，产生更灵活的变化，关于这一点下一节将详细介绍。

2. 可适配(Adaptable)的关键

STL算法非常灵活的一个关键因素之一在于STL仿函数的可配接性(adaptability)，即函数可以被配接器修饰，彼此相积木一样地串接。为了拥有配接能力，每一个仿函数必须定义自己的相应型别(associate types)，就像迭代器如果要融入整个STL大家庭，也必须依照规定定义自己的5个相应型别一样。这样做是为了让配接器能够获得函数的一些特性。相应型别都只是一些 typedef，所有必要操作在编译期就就全部完成了，对程序的执行效率没有任何影响，不带来任何额外负担。

仿函数相应型别主要用来表示函数的参数型别和返回值型别，为了方便，stl_function.h 中定义了两个基类，分别是 unary_function 和 binary_function，分别表示一元函数和二元函数，其中都是一些型别的定义，仿函数只需要继承其中一个类，就可以拥有配接能力了。

2.1 unary_function

该类用来封装一元函数的参数型别和返回值型别，其定义非常简单：

template <class _Arg, class _Result>
struct unary_function {
  typedef _Arg argument_type; // 参数型别
  typedef _Result result_type; // 返回值型别
};

仿函数可以继承该类，这样用户就可以取得该仿函数的参数型别，并以相同方法获得其返回值：

template <class _Tp>
struct negate : public unary_function<_Tp,_Tp> { // 仿函数 negate 继承 unary_function
  _Tp operator()(const _Tp& __x) const { return -__x; }
};
template <class _Predicate>
class unary_negate : public unary_function<typename _Predicate::argument_type, bool> {
protected:
  _Predicate _M_pred;
public:
  explicit unary_negate(const _Predicate& __x) : _M_pred(__x) {}
  bool operator()(const typename _Predicate::argument_type& __x) const { // 获取参数的型别argument_type
    return !_M_pred(__x);
  }
};

2.2 binary_function

该类用来封装二元函数的参数一、参数二型别和返回值类型，仅比一元函数多了一个输入参数型别的定义而已，其定义如下：

template <class _Arg1, class _Arg2, class _Result>
struct binary_function {
  typedef _Arg1 first_argument_type; // 参数一型别
  typedef _Arg2 second_argument_type; // 参数二型别
  typedef _Result result_type; // 返回值型别
};
template <class _Tp>
struct plus : public binary_function<_Tp,_Tp,_Tp> { // 仿函数 plus 继承 binary_function
  _Tp operator()(const _Tp& __x, const _Tp& __y) const { return __x + __y; }
};

3. STL 内建仿函数

STL 仿函数的分类，若以操作数的个数划分，可以分为一元和二元仿函数，若以功能划分，可以分为算术运算、关系运算、逻辑运算三大类，任何应用程序欲使用STL内建的仿函数，需要包含 <functional> 头文件，而这些仿函数的实际实现都在 stl_function.h 中。以下按功能分别介绍。

3.1 算术类(Arithmetic)仿函数

主要包括加法(plus)、减法(minus)、乘法(multiplies)、除法(divides)、取模(modulus)、否定(negation)等运算，除了否定以一元运算其他均为二元运算，如下：

template <class _Tp>
struct plus : public binary_function<_Tp,_Tp,_Tp> {
  _Tp operator()(const _Tp& __x, const _Tp& __y) const { return __x + __y; } // 加法，减、乘、除、取模类似
};
template <class _Tp>
struct negate : public unary_function<_Tp,_Tp> {
  _Tp operator()(const _Tp& __x) const { return -__x; }
};

仿函数搭配STL算法可以很灵活，例如对vector的每个元素求连乘如下：

accumulate(vct.begin(),vct.end(),1,multiplies<int>());

3.2 关系运算类(Relational)仿函数

主要有等于(equal_to)、不等于(not_equal_to)、大于(greater)、大于等于(greater_equal)、小于(less)、小于等于(less_equal)等六种运算，每一个都是二元运算，如下：

template <class _Tp>
struct equal_to : public binary_function<_Tp,_Tp,bool> {
  bool operator()(const _Tp& __x, const _Tp& __y) const { return __x == __y; } // 相等，其他类似 !=, >, <, >=, <=
};

例如，对vector进行递减顺序排序：

sort(vct.begin(),vct.end(),less<int>());

3.3 逻辑运算类(Logical)仿函数

主要是与(logical_and)、或(logical_or)、非(logical_not)三种逻辑运算，前两者为二元运算，后者为一元运算，如下：

template <class _Tp>
struct logical_and : public binary_function<_Tp,_Tp,bool> {
  bool operator()(const _Tp& __x, const _Tp& __y) const { return __x && __y; } // 与，或(||)类似
};
template <class _Tp>
struct logical_not : public unary_function<_Tp,bool>{
  bool operator()(const _Tp& __x) const { return !__x; } // 非
};

3.4 证同(identity)、选择(select)、投射(project)等非标准仿函数

这类仿函数都只是将参数原封不动的返回，其中某些仿函数对传回的参数有刻意的选择，或是刻意的忽略。之所以不在STL或其他泛型程序设计中直接使用原本及其简单的identity，project，select等操作，而要再划分一层出来，完全是为了间接性——间接性是抽象化的重要方法。另外，需要说明的是，这些仿函数并非C++标准，只是在SGI STL的实现中作为内部使用，一下是相关部分代码：

// 证同函数(identity)，任何数值通过此函数后不会有任何改变，它用于set实现中，用来指定RB-tree所需的
// KeyOfValue op，因为set元素的键值即实值，所以采用identity
template <class _Tp>
struct _Identity : public unary_function<_Tp,_Tp> {
  const _Tp& operator()(const _Tp& __x) const { return __x; }
};
// 选择函数(select)，接受一个pair返回其第一个元素，用于map实现中，用来指定RB-tree所需KeyOfValue op，
// 因为map以pair的第一个元素作为键值
template <class _Pair>
struct _Select1st : public unary_function<_Pair, typename _Pair::first_type> {
  const typename _Pair::first_type& operator()(const _Pair& __x) const {
    return __x.first;
  }
};
// 类似与select1st，接受pair返回第二个参数，SGI STL内部并未用到该函数
template <class _Pair>
struct _Select2nd : public unary_function<_Pair, typename _Pair::second_type>{
  const typename _Pair::second_type& operator()(const _Pair& __x) const {
    return __x.second;
  }
};
// 投射函数(project)，传回第一参数，忽略第二参数，SGI STL内部并未用到该函数
template <class _Arg1, class _Arg2>
struct _Project1st : public binary_function<_Arg1, _Arg2, _Arg1> {
  _Arg1 operator()(const _Arg1& __x, const _Arg2&) const { return __x; }
};
// 投射函数(project)，传回第二参数，忽略第一参数，SGI STL内部并未用到该函数
template <class _Arg1, class _Arg2>
struct _Project2nd : public binary_function<_Arg1, _Arg2, _Arg2> {
  _Arg2 operator()(const _Arg1&, const _Arg2& __y) const { return __y; }
};

除此之外，SGI STL实现中还有 constant_void_fun，constant_unary_fun， constant_binary_fun， subtractive_rng， mem_fun_t 等等，想深入详细了解的可以去看看源代码，还是很好理解的。

STL 适配器

1. 概述

适配器（adaptor/adapter）在STL组件的灵活运用功能上，扮演着轴承、转换器的角色，将一种容器或迭代器装换或封装成另一种容器或迭代器，例如基于deque容器的stack和queue。Adaptor这个概念，实际上是一种设计模式（design pattern），是《Design Pattern》一书中提及到的23个设计模式之一，其中对adaptor的定义如下：

将一个class的接口转换为另一个class的接口，使原本因接口不兼容而不能合作的classes，可以一起运作。

在STL中，除了上面提到的容器或迭代器的适配器之外，还可以对函数或更广义的仿函数使用适配器，改变其接口，这种称为function adaptor，相应的针对容器或迭代器的适配器则分别称为container adaptor，iterator adaptor，下面将分别介绍这三种适配器。

2. 容器适配器

容器适配器相对而言比较简单，比较典型的就是上面提到的低层由deque构成的stack和queue，其基本实现原理是，在 stack 和 queue 内部定义一个 protected 的 deque 类型的成员变量，然后只对外提供 deque 的部分功能或其异构，如 stack 的 push 和 pop 都是从 deque 的尾部进行插入和删除，而 queue 的 push 和 pop 分别是从尾部和头部进行插入和删除，这样 stack 和 queue 都可以看做是适配器，作用于容器 deque 之上的适配器。关于 stack 和 queue 的具体内容请参见之前将容器的文章深入理解STL源码(3.3) 序列式容器之deque和stack、queue。

3. 迭代器适配器

STL提供了许多作用于迭代器之上的适配器，如 insert iterator，reverse iterator，iostream iterator等，相关源代码主要在 stl_iterator.h 文件中。

3.1 insert iterator

其中 insert iterator 是将一般的迭代器的赋值（assign）操作变为插入（insert）操作，而其他的自增和自减操作则不做任何处理的返回当前迭代器本身，包括从尾部插入的 back_insert_iterator 和从头部插入的 front_insert_iterator ，尾部插入的 insert iterator 的定义主要内容如下：

template <class _Container>
class back_insert_iterator {
public:
  back_insert_iterator<_Container>&
  operator=(const typename _Container::value_type& __value) { // 赋值变为尾部插入
    container->push_back(__value);
    return *this;
  }
  back_insert_iterator<_Container>& operator*() { return *this; } // 一下操作均返回迭代器本身
  back_insert_iterator<_Container>& operator++() { return *this; }
  back_insert_iterator<_Container>& operator++(int) { return *this; }
};

3.2 reverse iterator

reverse iterator 则将一般的迭代器的行进方向逆转，是原本应该前进的 operator++ 变为后退操作，而 operator-- 变为前进操作，这样做对于需要从尾部开始遍历的算法非常有用。该迭代器的主要定义如下：

template <class _Iterator>
class reverse_iterator {
protected:
  _Iterator current;
public:
  typedef _Iterator iterator_type;
  typedef reverse_iterator<_Iterator> _Self;
public:
  _Self& operator++() { --current; return *this; } // 前置自增变为自减
  _Self operator++(int) { _Self __tmp = *this; --current; return __tmp; }
  _Self& operator--() { ++current; return *this; } // 前置自减变为自增
  _Self operator--(int) { _Self __tmp = *this; ++current; return __tmp; }
  _Self operator+(difference_type __n) const { return _Self(current - __n); }
  _Self& operator+=(difference_type __n) { current -= __n; return *this; }
  _Self operator-(difference_type __n) const { return _Self(current + __n); }
  _Self& operator-=(difference_type __n) { current += __n; return *this; }
  reference operator[](difference_type __n) const { return *(*this + __n); }
};

这种逆向的迭代器只用于那些具有双向迭代器的容器（如vector，list，deque等，而slist，stack，queue，priority queue等则不行）或需要逆向遍历的算法（如copy backward等）。

3.3 iostream iterator

iostream iterator 则将迭代器绑定到某个 iostream 对象上，有 istream_iterator 和 ostream_iterator ，分别拥有输入和输出功能。

以 istream iterator 为例，它将迭代器绑定到一个输入数据流对象（istream object）上，其实就是在 istream iterator 内部维护一个 istream member，用户对这个 istream iterator 所做的 operator++ 操作会被该迭代器变为这个 istream member 的输入操作 operator>>，这个迭代器是一个 input iterator，没有 operator-- 操作，核心实现如下：

template <class _Tp, class _CharT = char, class _Traits = char_traits<_CharT>,
          class _Dist = ptrdiff_t>
class istream_iterator {
public:
  typedef _CharT                         char_type;
  typedef _Traits                        traits_type;
  typedef basic_istream<_CharT, _Traits> istream_type;
  reference operator*() const { return _M_value; }
  pointer operator->() const { return &(operator*()); }
  istream_iterator& operator++() { _M_read(); return *this; } // ++ 变为 >>
  istream_iterator operator++(int)  { istream_iterator __tmp = *this; _M_read(); return __tmp; }
  bool _M_equal(const istream_iterator& __x) const
    { return (_M_ok == __x._M_ok) && (!_M_ok || _M_stream == __x._M_stream); }
private:
  istream_type* _M_stream;
  _Tp _M_value;
  bool _M_ok;
  void _M_read() {
    _M_ok = (_M_stream && *_M_stream) ? true : false;
    if (_M_ok) {
      *_M_stream >> _M_value; // 转变为输入操作（>>）
      _M_ok = *_M_stream ? true : false;
    }
  }
};

可以看到以上的迭代器均非一般意义上的迭代器了，而是一个经过适配了的特殊的迭代器。

4. 仿函数适配器

从上文中我们看到，container adaptor 内含一个container 的成员，iterator 内含一个 iterator 或 iostream 成员，然后对这些成员的标准接口进行了一定的改造，从而使之变成一个新的 container 或 iterator，满足新的应用环境的要求。而仿函数的适配器也是类似的，其实就是在 function adaptor 内部定义了一个成员变量，它是原始 functor 的一个对象，相关源代码主要在 stl_function.h 文件中。

STL中标准的 functor adaptor 包括对返回值进行逻辑否定的 not1，not2；对参数进行绑定的 bind1st，bind2nd；用于函数合成的 compose1，compose2 （非STL标准，SGI私有）；用于函数指针的 ptr_fun；用于成员函数指针的 mem_fun，mem_fun_ref 等。其中逻辑否定、参数绑定、函数合成的比较简单，如下：

// not1其实是对unary_negate函数的一个简单的封装，定义了一个unary_negate类型匿名对象（函数）
inline unary_negate<_Predicate> // 实际效果：!pred(param)
not1(const _Predicate& __pred){ return unary_negate<_Predicate>(__pred);}
inline binary_negate<_Predicate> // 实际效果：!pred(param1,param2)
not2(const _Predicate& __pred){ return binary_negate<_Predicate>(__pred); }
inline binder1st<_Operation> // 实际效果：op(x,param)
bind1st(const _Operation& __fn, const _Tp& __x) {
  return binder1st<_Operation>(__fn, _Arg1_type(__x));
}
inline binder2nd<_Operation> // 实际效果：op(param,x)
bind2nd(const _Operation& __fn, const _Tp& __x) {
  return binder2nd<_Operation>(__fn, _Arg2_type(__x));
}
inline unary_compose<_Operation1,_Operation2> // 实际效果：op1(op2(param))
compose1(const _Operation1& __fn1, const _Operation2& __fn2) {
  return unary_compose<_Operation1,_Operation2>(__fn1, __fn2);
}
inline binary_compose<_Operation1, _Operation2, _Operation3> // 实际效果：op1(op2(param),op3(param))
compose2(const _Operation1& __fn1, const _Operation2& __fn2, const _Operation3& __fn3) {
  return binary_compose<_Operation1,_Operation2,_Operation3>
    (__fn1, __fn2, __fn3);
}

用于函数指针的 ptr_fun 适配器使得我们可以将一般函数当做仿函数使用，就像原生指针可以当做迭代器传给STL算法一样，它的实际效果相当如 fp(param) 或 fp(param1,param2) ，前者定义如下：

template <class _Arg, class _Result>
class pointer_to_unary_function : public unary_function<_Arg, _Result> {
protected:
  _Result (*_M_ptr)(_Arg);
public:
  pointer_to_unary_function() {}
  explicit pointer_to_unary_function(_Result (*__x)(_Arg)) : _M_ptr(__x) {}
  _Result operator()(_Arg __x) const { return _M_ptr(__x); }
};
template <class _Arg, class _Result>
inline pointer_to_unary_function<_Arg, _Result> // 返回值型别
ptr_fun(_Result (*__x)(_Arg)) { // 对pointer_to_unary_function 的封装
  return pointer_to_unary_function<_Arg, _Result>(__x);
}

用于成员函数指针的 mem_fun 适配器使得我们可以将成员函数当做仿函数使用，于是成员函数可以搭配各种泛型算法，而当使用父类的虚拟成员函数作为仿函数时，还可以使用泛型算法完成所谓的多态调用（polymorphic function call），这是泛型（genericity）与多态（polymorphism）之间的结合。另外需要注意的是，虽然多态可以对指针或引用起作用，但STL容器只支持“实值语意”，不支持“引用语意”，及容器的内容应该为实值而非引用（类似于vecotr<X&> vc 这种）。一下是 mem_fun 的具体定义（还有很多个版本，这里只是最简单的一个）：

// 无任何参数，通过pointer调用，non-const成员函数
template <class _Ret, class _Tp>
class mem_fun_t : public unary_function<_Tp*,_Ret> {
public:
  explicit mem_fun_t(_Ret (_Tp::*__pf)()) : _M_f(__pf) {}
  _Ret operator()(_Tp* __p) const { return (__p->*_M_f)(); }
private:
  _Ret (_Tp::*_M_f)();
};
template <class _Ret, class _Tp>
inline mem_fun_t<_Ret,_Tp> // 返回类型
mem_fun(_Ret (_Tp::*__f)()) { return mem_fun_t<_Ret,_Tp>(__f); } // mem_fun_t的匿名对象

深入理解STL源码学习笔记

STL 简介

0.两个问题

1.STL 简史

2.STL 六大组件

2.1 Memory Allocation

2.2 Iterators

2.3 Containers

2.4 Algorithm

2.5 Function Objects

2.6 Adaptors

3. STL 各组件间的关系

4. SGI STL源码结构

5. 参考及推荐

推荐阅读

源码阅读与分析工具

参考

STL 空间配置器

1. Allocator 的标准接口

2. SGI STL 内存分配失败的异常处理

3. SGI STL 内置轻量级内存池的实现

4. SGI STL 内存池在多线程下的互斥访问

STL 迭代器

1. 迭代器的设计思维

2. STL 迭代器的分类与标准接口

2.1 STL 迭代器的分类

2.2 STL迭代器的标准接口

3. 迭代器相应型别与Traits编程技巧

3.1 迭代器相应型别

3.2 Traits 编程技巧

4. SGI 中的 __type_traits

STL 容器

序列式容器之vector

1. 容器

2. vector 及其数据结构

3. vector 的配置器

4. vector 的迭代器

5. vector 的常用操作

序列式容器之list

1. list 和 slist

2. list 的数据结构

3. list 的配置器

4. list 的迭代器

5. list 的常用操作

序列式容器之deque和stack、queue

1. deque 概述

2. deque 的数据结构

3. deque 的配置器

4. deque 的迭代器

5. deque 的常用操作

6. 基于deque 的 stack 和 queue

序列式容器之heap和priority Queue

1. 概述

2. priority queue 的数据结构

3. push heap 算法

4. pop heap 算法

5. make heap 算法

6. 基于 heap 的 priority queue

关联式容器之红黑树

0. 关联式容器

1. 树与二叉搜索树

2. RB-tree的定义及数据结构

3. RB-tree的迭代器

4. RB-tree的插入操作

4.1 基本插入操作

4.2 调整RB-tree使之恢复平衡

5. RB-tree的删除操作

6. RB-tree的查询操作

小结

关联式容器之set和multiset

1. set 简介

2. set 的实现

3. multiset

关联式容器之map和multimap

1. map 简介

2. map 的实现

3. multimap

关联式容器之hashtable

1. hashtable 简介

线性探测